គណិតវិទ្យា
តក្កវិទ្យា
១.សំណើ
និយមន័យៈ សំណើ គឺជាអំណះអំណាងទាំងឡាយណាដែលគេអាចសម្រេចថាពិត ឬក៏ មិនពិត ។
-
គេតាងឈ្មោះនៃសំណើដោយអក្សរ p, q, r, s,... ។
-
បើ p ជាសំណើពិតនោះ p មានតម្លៃភាពពិតស្មើនឹង 1 គឺ ត.(p)=1
-
បើ p ជាសំណើមិនពិតនោះpមានតម្លៃភាពពិតស្មើនឹង ០ គឺ ត.(p) = 0
២. ឈ្នាប់តក្កវិទ្យា
ក. ឈ្នាប់និង ( `wedge` )
គេកំណត់សរសេរ p `wedge` q អានថា p និង q
សំណើ p `wedge` q ពិតតែក្នុងករណីសំណើ p និង q ពិត
ខ.ឈ្នាប់ឬ ( `vee` )
-
គេកំណត់សរសេរ p `vee` q អានថា p ឬ q
-
សំណើ p `vee` q មិនពិតតែក្នុងករណីសំណើ p និង q មិនពិតទាំងពីរ
គ. ឈ្នាប់មិន ( `overline` )
-
គេកំណត់សរសេរ `overline{P}` អានថា មិន p
-
សំណើ p និង សំណើ `overline{P}` មានតម្លៃភាពពិតខុសគ្នា។
ឃ. ឈ្នាប់នាំឱ្យ (`Rightarrow`)
-
គេកំណត់សរសេរ p `Rightarrow` q អានថា p នាំឲ្យ q
-
សំណើ p `Rightarrow` q មិនពិតតែក្នុងករណីសំណើ p ពិត និង q មិនពិត ក្រៅពីនេះវាជាសំណើពិត។
-
p ជាលក្ខខណ្ឌគ្រប់គ្រាន់ដើម្បីឲ្យ q។
-
q ជាលក្ខខណ្ឌចាំបាច់ដើម្បីឲ្យ p ។
-
ង. ឈ្នាប់សមមូល ( `Leftrightarrow` )
-
គេកំណត់សរសេរ p `Leftrightarrow` q អានថា p សមមូល q
-
សំណើ p `Leftrightarrow` q ពិតតែក្នុងករណីដែលសំណើ p និងសំណើ q មានតម្លៃភាពពិតដូចគ្នា ។
-
p ជាលក្ខខណ៏ចាំបាច់ និងគ្រប់គ្រាន់ដើម្បីឲ្យ q ។
-
ជាទូទៅ p `Leftrightarrow` q = (p `Rightarrow` q) `wedge` (q `Rightarrow` p)
-
៣. ប្រភេទនៃសម្រាយបញ្ជាក់
ក. សម្រាយបញ្ជាក់ដោយផ្ទល់
ប្រភេទនៃសម្រាយបញ្ជាក់នេះគឺជាការស្រាយបញ្ជាក់ត្រង់ៗទៅតាមអ្វីដលគេចង់បាន។
ខ. សម្រាយបញ្ជាក់តាមសំណើផ្ទុយពីសម្មតិកម្ម
របៀបដោះស្រាយ
-
ឧបមាថា គេចង់បង្ហាញសំណើ p `Rightarrow` q ពិត
-
ជំហ៊ានទី១ ត្រូវកំណត់សំណើ p និងសំណើ q ឲ្យបានត្រឹមត្រូវ។
-
ជំហ៊ានទី២ ត្រូវកំណត់សំណើ `overline{P}` និងសំណើ `overline{q}` ។
-
ជំហ៊ានទី៣ គេផ្តើមពី `overline{q}` បញ្ចាក់រហូតគេបានសំណើ `overline{P}`ដែលជាសំណើផ្ទុយពីសម្មតិកម្ម គឺមានន័យថាគេបានបង្ហាញថា `overline{q} Rightarrow overline{P}` ពិត
ដូចនេះគេបានសំណើ p `Rightarrow` q ពិត ។
គ. សម្រាយបញ្ជាក់ផ្ទុយពីការពិត
របៀបដោះស្រាយ
-
ជំហ៊ានទី១ តាង p ជាសំណើដែលត្រូវបង្ហាញ។
-
ជំហ៊ានទី២ ត្រូវកំណត់សំណើ `overline{P}` ។
-
ជំហ៊ានទី៣ ឧបមាថាសំណើ `overline{P}` ពិត រួចបកស្រាយបន្តបន្ទាប់រហូតដល់បានលទ្ឋផលផ្ទុយពីទ្រឹស្តីគណិតវិទ្យា។ គេបានសំណើ `overline{P}` មិនពិត។ ដូចនេះសំណើ p ពិត (ព្រោះតម្លៃភាពពិតរវាងសំណើ p និង `overline{P}` មានតម្លៃផ្ទុយគ្នា) ។
ឃ. សម្រាយបញ្ជាក់តាមទ្វេលក្ខខណ្ឌ
របៀបដោះស្រាយ
-
ជំហ៊ានទី១ បង្ហាញលក្ខខណ្ឌចាំបាច់ p `Rightarrow` q
-
ជំហ៊ានទី២ បង្ហាញលក្ខខណ្ឌគ្រប់គ្រាន់ q `Rightarrow` p
ង. សម្រាយបញ្ជាក់តាមឧទាហរណ៍ផ្ទុញ
វិធីនេះតម្រូវឲ្យគេរកឧទាហរណ៍មួយមកបញ្ជាក់ថាសំណើដែលត្រូវបង្ហាញជាសំណើមិនពិត ។
សំណុំ
-
សំណុំ គឺជាបណ្ដុំនៃវត្ថុ ដែលកំណត់ដោយលក្ខខណ្ឌជាក់លាក់។
-
ចំនួនធាតុនៃសំណុំ A តាងដោយ n(A)។
-
សំណុំទទេ គឺជាសំណុំដែលគ្មានធាតុសោះ ហើយតាងដោយ `emptyset` ។
-
ការកំណត់សំណុំមានពីររបៀប៖ កំណត់តាមការរៀបរាប់ឈ្មោះធាតុ និង កំណត់តាមលក្ខណៈរួមនៃធាតុ។
-
-
សំណុំរាប់អស់ជាសំណុំដែលមានចំនួនធាតុជាចំនួនកំណត់។
-
សំណុំអនន្តថាសំណុំដែលមានចំនួនធាតុច្រើនរាប់មិនអស់។
-
-
សំណុំស្មើគ្នាកាលណាសំណុំទាំងពីរមានបញ្ជីឈ្មោះធាតុដូចគ្នា។
-
A ជាសំណុំរង់នៃ B លុះត្រាតែគ្រប់ x `in` A នោះ x `in` B
-
បើ A ជាសំណុំនៃ B លុះត្រាតែគ្រប់ n(A) `le` n(B)។
-
បើ A ជាសំណុំរងផ្ទាល់នៃ B នោះ n(A) `lt` n(B)។
-
សំណុំសកលគឺជាសំណុំដែលមានគ្រប់ធាតុដែលគេបានជ្រើសរើសយកមកសិក្សា។
-
សំណុំរងបំពេញ `overline{A}` = { x / x `in` A , x `in` U}
-
សំណុំប្រសព្វ A `cap` B = { x `in` A និង x `in` B }
-
ប្រជុំរូបមន្តគណិតវិទ្យា
-
សំណុំប្រជុំ A `cup` B = { x `in` A ឬ x `in` B }
-
សំណុំ A និង B ជាសំណុំដាច់គ្នាលុះត្រាតែ A `cap` B = `emptyset` ។
-
ចំពោះគ្រប់សំណុំ A និងសំណុំសកល U គេបាន៖ A `cap overline {A}` = `emptyset` , A `cup overline{A}` = U ។
-
បើ A និង B ជាសំណុំរាប់អស់នោះគេបានរូបមន្ត៖ n(A `cup` B)= n(A)+n(B)-n(A `cap` B)
-
លក្ខណៈ DeMogan៖ `overline{A cup B}` = `overline{A} cap overline{B}` ; `overline{A cap B}` = `overline{A} cup overline{B}`
-
លក្ខណៈផ្តុំ
-
1/ A `cap` (B `cap` C) = ( A `cap` B) `cap` C
-
2/ A `cup` (B `cup` C) = (A `cup` B) `cup` C
-
-
លក្ខណៈបំបែក
1/ A `cap` (B `cup` C) = ( A `cup` B) `cup` (A `cap` C)
2/ A `cup` (B `cap` C) = (A `cup` B) `cap` (A `cup` C)
ចំនួន ពហុធា ប្រព័ន្ឋរបាប់
១.ចំនួន
បន្ទាត់ចំនួន
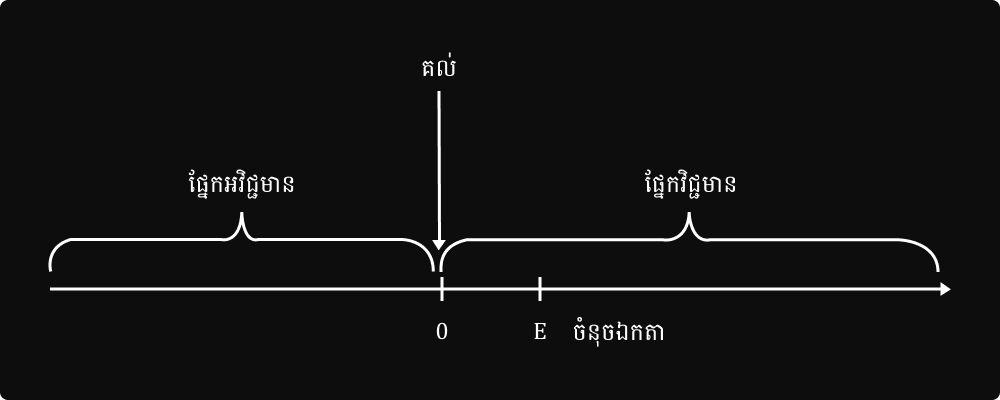
លក្ខណៈនៃតម្លៃដាច់ខាត
-
|a|=a បើ a `ge` 0
-
|a|=- a បើ a `lt` 0
សំណុំចំនួនគត់ធម្មជាតិ IN = {1, 2 , 3 ,...}
សំណុំចំនួនគត់រ៉ឺឡាទីហ្វ Z = {...,-2,-1,0,1,2,...}
ចំនួនសនិទានមានទម្រង់ ដែល mn ដែល m និង n ជាចំនួនគត់រ៉ឺឡាទីប
សំណុំចំនួនសនិទានតាងដោយ Q
គ្រប់ចំនួនពិតវិជ្ជមាន a និង b គេបាន a < b `Leftrightarrow` `sqrt{a} lt sqrt{b}`
ចំពោះ a > b និង b > 0 គេបាន៖ `sqrt{ab}`= `sqrt{a}`.`sqrt{b}` , `sqrt{a^2}` =`(sqrt{a})^2` , `sqrt{a/b}`=`sqrt{a}/ sqrt{b}`
ទម្រង់ពន្លាតនៃប្រព័ន្ឋរបាប់គោល 10 មានរាង៖ `abcd_10 = a times 10^3 +b times 10^2+c times 10+d`
ទម្រង់ពន្លាតនៃប្រព័ន្ឋរបាប់គោល 2 មានរាង៖ `abcd_2 = a times 2^2+b times 2^2+c times 2+d`
២. ឯកធា និង ពហុធា
ឯកធាគឺជាកន្សោមដែលប្រមាណវិធីលើអថេរមានតែវិធីគុណ និង ស្វ័យគុណដែលមាននិទស្សន្ដគត់វិជ្ជមាន ឬសូន្យ។
ឯកធាដូចគ្នា គឺជាឯកតាដែលមានផ្នែកអថេរដូចគ្នា។
ដឺក្រេនៃឯកធា ជាផលបូកនិទស្សន្តរបស់អថេរនីមួយៗនៃឯកធា។
ពហុធា ជាផលបូកនៃច្រើនឯកធាខុសៗគ្នា។
ដឺក្រេនៃពហុធា គឺជាដឺក្រេរបស់តួដែលមានដឺក្រេខ្ពស់ជាងគេ។
៣. ប្រមាណវិធីលើ ពហុធា
ដើម្បីបូក ឬ ដកពីរពហុធា គេត្រូវបូក ឬ ដកឯកធាដែលដូចគ្នា។
ដើម្បីគុណពហុធា និង ពហុធាគេយកតួនីមួយៗនៃពហុធាទីមួយគុណ គ្រប់តួនៃពហុធាទីពីរ រួចធ្វើប្រមាណវិធី។
៤. រូបមន្ត
-
`(a+b)^2 = a^2+2ab+b^2`
-
`(a-b)^2 = a^2-2ab+b^2`
-
`(a-b)(a+b) = a^2-b^2`
-
`(a + b + c)^2= a^2+b^2+c^2+2ab+2bc+2ca`
-
`(a+b)^3 = a^3+3a^2b+3ab^2+b^3`
-
`(a-b)^3 = a^3-3a^2b+3ab^2-b^3`
-
`(a+b)(a2-ab+b2)=a^3-b^3`
-
`(a-b)(a2+ab+b2)=a^3+b^3`
-
`acx^2+(ad+bc)x+bd=(ax+b)(cx+d)`
៥. ប្រមាណវិធីចែកពហុធា
ឧបមាថាគេមានកន្សោមពីរ A និង B ដែលមានអថេរដូចគ្ន ហើយមានដឺក្រេរៀងគ្នា m និង n ។ បើ m `ge`n គេអាចរកកន្សោមពីជគណិតពីរ Q និង R ដែល A=B `times` Q+R។ ដឺក្រេនៃ R តូចជាងដឺក្រេនៃ B។ Qជាផលចែក ហើយ R ជាសំណល់នៃក្នុងវិធីចែក។ ផលចែក Q មានដឺក្រេ m-n។
បើ R = 0 គេបាន A = B `times` Q នោះគេថា A ចែកដាច់នឹង B
៦. តួចែករួមធំបំផុត និង ពហុគុណរួមតូចបំផុត
តួចែករួមធំបំផុតនៃកន្សោម A និង B គឺជាផលគុណកត្តារួមដែលមាននិទស្សន្តតូចជាងគេ។
ពហុគុណរួមតូចបំផុត គឺជាផលគុណគ្រប់កត្តារួមដែលមាននិទស្សន្តធំជាងគេ ។
៧ . វិធាន
ដើម្បីគណនាតួចែករួមធំបំផុត៖
-
១-ដាក់ផលគុណកត្តា គ្រប់តួទាំងអស់
-
២-ជ្រើសរើសយកតែកត្តារួមដែលមាននិទស្សន្តតូចជាងគេ។
-
៣-តួចែករួមធំបំផុត ជាផលគុណនៃកត្តារួមទាំងនោះ ។
ដើម្បីគណនាតួចែករួមតូចបំផុត៖
-
១.ដាក់ជផលគុណកត្តា គ្រប់តួទាំងអស់
-
២-ជ្រើសរើសយកតែកត្តាមិនរួម និង កត្តារួមដែលមាននិទស្សនធំជាងគេ។
-
៣-ពហុគុណរួមតូចបំផុត ជាផលគុណនៃកត្តាទាំងនោះ ។
៨. ប្រមាណវិធីបូក ឬ ដកកន្សោមប្រភាគ
`A/C + B/C = (A + B)/C` និង `A/C - B/C = (A-B)C` ដែល `C ≠ 0` ។
៩. វិធាន
ដើម្បីធ្វើ វិធីបូក ឬដកកន្សោមប្រភាគគេត្រូវ៖
១.តម្រូវប្រភាគនីមួយៗឲ្យមានភាគបែងរួមដូចគ្នា
២-ធ្វើប្រមាណវិធីបូក ឬដកនៃភាគយក រក្សាទុកភាគបែងរួម
៣-សម្រួលលទ្ឋផល
១០. ប្រមាណវិធីគុណ និង ប្រមាណវិធីចែក
`A/C times B/C = (A times C)/(B times D)` និង `A/B div C/D = (A times D)/(B times C)` ដែល `B, C, D ne 0` ។
១១. វិធាន
ដាក់ភាគយក និង ភាគបែងនៃកន្សោមទាំងអស់ជាផលគុណកត្តា
សម្រួលកន្សោមប្រភាគនីមួយៗ
ធ្វើប្រមាណវិធីគុណ ឬ វិធីចែកតាមរូបមន្តខាងលើ។
សមីការ និង វិសមីការ
១. សមីការដឺក្រេទីពីរមានមួយអញ្ញាត
ក - និយមន័យ
សមីការដែលមានរាងទូទៅ ` ax^2 + bx + c = 0 ` ហៅថាសមីការដឺក្រេទីពីរ មានមួយអញ្ញាតដែល x ជាអញ្ញាត ហើយលេខមេគុណ a,b,c ជាចំនួនថេរ និង `a ne 0` ។
ខ - ដំណោះស្រាយសមីការដឺកទីពីរ
សន្មតថាគេមានសមីការ `ax^2 + bx + c = 0 , a ne 0`
ឌីសគី្រមីណង់សមីការ ` Delta = b^2 - 4ac`
-
បើ ` Delta > 0` សមីការមានឬសពីរជាចំនួនពិតផ្សេងគ្នាគឺ៖ `x_1= (-b+ sqrt(Delta))/(2a) , x_2= (-b+ sqrt(Delta))/(2a) ,`
-
បើ ` Delta = 0` សមីការមានឬសឌុប៖ ` x_1= x_2= b/(2a)`
-
បើ ` Delta < 0 ` សមីការមានឬសពីរផ្សេងគ្នាជាចំនួនកុំផ្លិចឆ្លាស់គ្នា៖ ` x_1=(-b+isqrt(-Delta))/(2a) , x_2=(-b-isqrt(-Delta))/(2a) `
គ - ទំនាក់ទំនងឬស និង លេខមេគុណ
បើ និង ជាប្ញសរបស់សមីការ `ax^2` + bx + c = 0, a `ne` 0 នោះគេមាន៖
-
ផលបូកឬស `S=alpha + beta = -a/b`
-
ផលគុណឬស `P = alpha . beta=c/a`
ឃ - មុធាគណនាឬសនៃសមីការដឺកទីពីរងាយ
ឧបមាថាគេមានសមីការដឺក្រេទីពីរ `ax^2 + bx + c = 0 , a ne 0`
-
បើ a + b + c = 0 សមីការមានប្ញស `x_1= 1 , x_2 = b/a`
-
បើ b = a + c សមីការមានប្ញស `x_1= -1 , x_2 = - b/a`
ង - រូបមន្តដាក់ជាផលគុណកត្តា
បើ `alpha` និង `beta` ជាឬសរបស់សមីការ `ax^2 + bx + c` = 0, `a ne` 0 នោះគេបាន៖ `ax^2 + bx + c = a(x- alpha)(x-beta)`
ច - បង្កើតសមីការដឺកទីពីរ
បើគេដឹងផលបូក ` alpha + beta = S` និង ផលគុណ `alphabeta` = P នោះ `alpha` និង `beta` ជាឬសសមីការដឺក្រេទីពីរ `x^2-Sx+P` =0។
២-វិសមភាព
ក - លក្ខណៈវិសមភាព
-
ចំពោះគ្រប់ចំនួនពិត a, b, c បើ a>b នោះគេបាន a+c > b+c ឬ a-c>b-c ។
-
ចំពោះគ្រប់ចំនួនពិត a, b, c គេមាន :
-
បើ a>b និង c > 0 នោះ ac > bc
-
បើ a>b និង `clt` 0 នោះ ac ` lt `bc
-
ខ - វិសមភាពមធ្យមនព្វន្ត និង មធ្យមធរណីមាត្រ
ចំពោះគ្រប់ចំនួនពិត a≥០ និង b≥0 គេមានៈ
-
`(a+b)/2 ge sqrt(ab)` ។
វិសមភាពនេះក្លាយជាសមភាពលុះត្រាតែ a=b។
៣ - វិសមីការតម្លៃដាច់ខាត
បើ `alpha gt` 0 នោះគបាន
-
| ax + b | < `alpha iff` ax+b < `alpha` និង ax + b> - `alpha`
-
| ax+b |> `alpha iff` ax+b > `alpha` ឬ ax + b < - `alpha`
-
| ax+b |= `alpha iff` ax+b= `pm alpha`
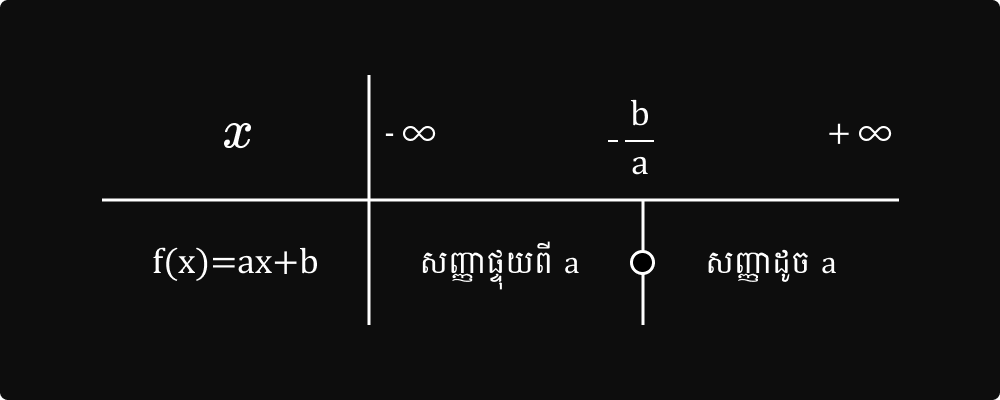
៤ - សញ្ញារបស់ទ្វេធដឺក្រេទីមួយ
ចំពោះទ្វេធា f(x)=ax+b មាន x=-ba ជាឬស គេកំណត់សញ្ញាទ្វេធានេះទៅតាមសញ្ញារបស់ a ដូចតារាងខាងក្រោម៖
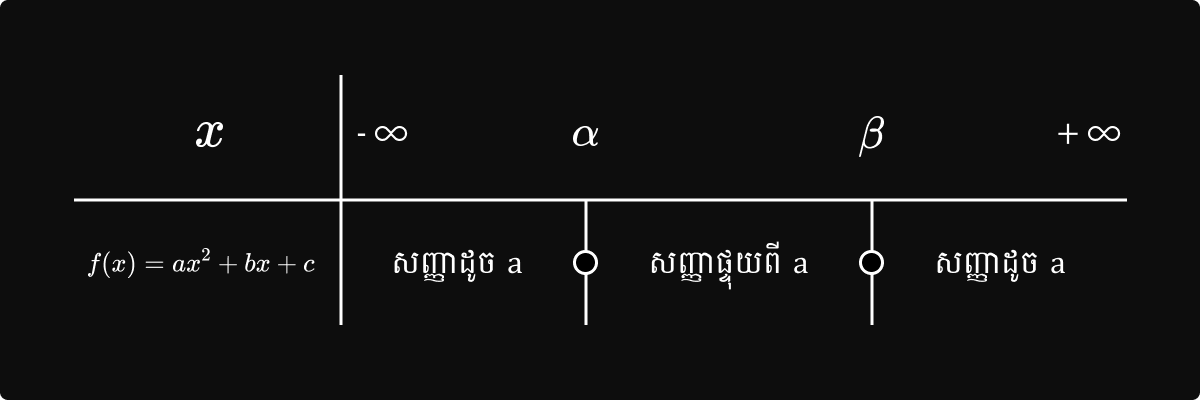
៥ - សញ្ញារបស់ត្រីធាដឺក្រេទីពីរ
ចំពោះត្រីធា `f(x)=ax^2+bx+c` មានឬសពីរ `alpha` និង `beta` ដែល `alpha` < `beta` ។
៦ - ចម្លើយវិសមីការដឺក្រេទីពីរ
ករណី `Delta` > 0 និង a > 0 មានឬស `alpha` , `beta`( `alpha` < `beta`)'
-
`ax^2+bx+c` > 0 មានចម្លើយ x < `alpha` , x> `beta` ។
-
`ax^2+bx+c < ` 0 មានចម្លើយ `alpha` < x < `beta` ។
-
`ax^2+bx+c ge`0 មានចម្លើយ x `le alpha` , `ge beta` ។
-
`ax^2+bx+c le`0 មានចម្លើយ `alpha le x le beta` ។
ករណី `Delta` = 0 និង a > 0 មានឬសឌុប
-
`ax^2+bx+c` > 0 មានចម្លើយគ្រប់ចំនួនពិតលើកលែងតែ `x=-b/(2a)`
-
`ax^2+bx+c` < 0 គ្មានចម្លើយ។
-
`ax^2+bx+c ge`0 មានចម្លើយគ្រប់ចំនួនពិតទាំងអស់។
-
`ax^2+bx+c le `0 មានចម្លើយ `x=-b/(2a)`។
ករណី `Delta` < 0 និង a> 0 មានឬសជាចំនួនកុំផ្លិច
-
`ax^2+bx+c` > 0 មានចម្លើយគ្រប់ចំនួនពិតទាំងអស់។
-
`ax^2+bx+c` < 0 គ្មានចម្លើយ។
-
`ax^2+bx+c ge`0 មានចម្លើយគ្រប់ចំនួនពិតទាំងអស់។
-
`ax^2+bx+c le `0 គ្មានចម្លើយ។
ស្វ៉ីតនៃចំនួនពិត
I. ស្វ៉ីតនព្វន្ត និង ស្វ៉ីតធរណីមាត្រ
១. ស្វ៉ីតចំនួនពិត
ស្វ៉ីតនៃចំនួនពិតគឺជាអនុគមន៍លេខដែលកំណត់ពីសំណុំ IN ទៅ សំណុំ IR។ គេកំណត់សរសេរស្វ៉ីតមួយដោយ `(U_n)` ឬ `(U_n)_( nin IN)` ដែល `U_n= f(n)`
២. អថេរភាពនៃស្វ៉ីត
ក. ស្វ៉ីតកើន
គេថាស្វ៉ីត `(U_n)` ជាស្វ៉ីតកើនលើ IN កាលណាគ្រប់ `n in IN` គេមាន `U_(n+1)> U_n`
ខ. ស្វ៉ីតចុះ
គេថាស្វ៉ីត `(U_n)` ជាស្វ៉ីតចុះលើ IN កាលណាគ្រប់ `n in IN` គេមាន `U_(n+1)< U_n`
គ. ស្វ៉ីតម៉ូណូតូន
គេថាស្វ៉ីត `(U_n)` ជាស្វ៉ីតម៉ូណូតូនកាលណាវាជាស្វ៉ីតកើនជានិច្ច ឬជាស្វ៉ីតចុះជានិច្ច។
៣. ស្វ៉ីតទាល់
ក. ស្វ៉ីតទាល់លើ
គេថាស្វ៉ីត `(U_n)` ជាស្វ៉ីតទាល់លើកាណាមានចំនួនពិត M ដែលបំពេញលក្ខ័ខណ្ឌ័ `foralln in IN : U_n le M`។
ខ. ស្វ៉ីតទាល់ក្រោម
គេថាស្វ៉ីត `(U_n)` ជាស្វ៉ីតទាល់ក្រោមកាណាមានចំនួនពិត M ដែលចំពោះ `foralln in IN : U_n ge M`។
គ. ស្វ៉ីតទាល់
គេថាស្វ៉ីត `(U_n)` ជាស្វ៉ីតទាល់កាណាវាជាស្វ៉ីត ទាលើលើផង និងទាល់ក្រោមផង។
៤. ស្វ៉ីតខួប
គេថាស្វ៉ីត `(U_n)` ជាស្វ៉ីតខួបដែលមានខួបស្មើ p កាលណាចំពោះ `foralln in IN : U_(n+p)=U_n ` , `p in IN*`។
៥. ស្វ៉ីតនព្វន្ត
ស្វ៉ីតនព្វន្ត ជាស្វ៉ីតនៃចំនួនពិតដែលមានតួនីមួយៗ (ក្រៅពីតួទីមួយ) ស្មើនឹងតួមុនបន្ទាប់បូកចំនួនថេរ d មួយហៅថាផលសងរួម ឬរេសុងនៃស្វ៉ីតរូបមន្តផលសងរួម `d=u_(n+1)-u_n`។
តួទី n នៃស្វីតនព្វន្ត ` u_n=u_1+(u-1)d`
ផលបូក n តូដំបូងនៃស្វ៉ីតនព្វន្ត
`S_n=sum_{k=1}^n (u_k)=u_1+u_2+u_2+u_3+...+u_n=(n(u_1+u_2))/2`
៦. ស្វ៉ីតធរណីមាត្រ
ស្វ៉ីតធរណីមាត្រ គឺជាស្វ៉ីតនៃចំនួនពិតដែលមានតួនីមួយៗ (ក្រៅពីតួទីមួយ) ស្មើនឹងតួមុនបន្ទាប់គុណនឹងចំនួនថេរ q មួយដែលខុសពីសូន្យ។ ចំនួនថេរ q ហៅថាផលធៀបរួម ឬរេសុងនៃស្វ៉ីត។
រូបមន្តផលធៀបរួម `q=(u_n+1)/u_n`។
តួទី n នៃស្វីតធរណីមាត្រ `u_n=u_1 times q^(n-1)`
ផលបូក n តួដំបូងនៃស្វ៉ីតធរណីមាត្រ
`S_n=sum_{k=1}^n (u_k)=u_1+u_2+u_2+u_3+...+u_n=(q_n-1)/(q-1)`
រូបមន្តផលបូកស្វ៉ីតនព្វន្តមានលំដាប់ខ្ពស់
`sum_{k}^n=1+2+3+...+n=n(n+1)/2`
`sum_{k^2}^n=1^2+2^2+3^2+...+n^2=(n(n+1)(2n+1))/6`
`sum_{k^3}^n=1^3+2^3+3^3+...+n^3=(n^2(n+1)^2)/4`
II. របៀបគណនាផលបូកតួនៃស្វ៉ីតផ្សេងៗ
១. និម្មិតសញ្ញា `sum` សម្រាប់ផលបូកនៃស្វ៉ីត
ផលបូក n តួដំបូងនៃស្វ៉ីត `u_1,u_2,u_2,.....,u_n` កំណត់តាងដោយ៖
`S_n=sum_{k = 1}^n (u_k)=u_1+u_2+u_3+...+u_n`
២. លក្ខណៈផលបូកតួនៃស្វ៉ីត
`sum_{k=1}^n (lambda)= lambda + lambda + lambda + ...+ lambda =nlambda`
`sum_{k=1}^n (lambda u_k)=lambda sum_{k=1}^n (u_k) (lambda `ជាចំនួនថេរ)
`sum_{k=1}^n (u_k + v_k + w_k)=sum_{k=1}^n (u_k) +sum_{k=1}^n ( v_k ) + sum_{k=1}^n ( w_k)`
`sum_{k=1}^n (u_k + v_k) ^2=sum_{k=1}^n (u_k)^2 +2 sum_{k=1}^n ( u_k v_k ) + sum_{k=1}^n (v_k)^2`
៣. របៀបគណនាផលបូកស្វ៉ីតដែលមានទម្រង់៖
`S_n=1^p+2^p+3^p+....+n^p ` ដែល p= 1; 2; 3;....
ដើម្បីគណនាផលបូកនេះគេត្រូវអនុវត្តនៃ៍តាមជំហានខាងក្រោម៖
គណនា `(n+1)^(p+1)-n^p`
ឲ្យតម្លៃ n = 1; 2; 3;....;n
ធ្វើវិធីបូក។
៤. របៀបគណនាផលបូកស្វ៉ីតដែលមានទម្រង់៖
`S_n=1/(a_1a_2)+1/(a_2a_3)+1/(a_3a_4)+....+1/(a_na_(n+1))` ដែល `a_(n+1)-a_n = d ` ថេរហើយ `d ne` 0។
ដើម្បីគណនាផលបូកនេះគេត្រូវ៖
បម្លែងតួរ `1/(a_na_(n+1))=1/d.(a_(n+1)-a_n)/(a_na_(n+1))=1/d(1/a_n-1/(a_(n+1)))`
ឲ្យតម្លៃ n = 1; 2; 3;....;n
ធ្វើវិធីបូក។
៥. របៀបគណនាផលបូកស្វ៉ីតដែលមានទម្រង់៖
`S_n=1/(a_1a_2a_3)+1/(a_2a_3a_4)+1/(a_3a_4a_5)+....+1/(a_na_(n+1)a_(n+2))` ដែល` a_(n+2)-a_n=d` ថេរហើយ d`ne`0។
ដើម្បីគណនាផលបូកនេះគេត្រូវ៖
-
បម្លែងតួរ `1/(a_na_(n+1)+a_(n+2))=1/d.(a_(n+2)-a_n)/(a_na_(n+1)+a_(n+2))=1/d(1/(a_na_(n+1))-1/(a_(n+1)+a_(n+2)))`
-
ឲ្យតម្លៃ n = 1; 2; 3;....;n
-
ធ្វើវិធីបូក។
៦. របៀបគណនាផលបូកស្វ៉ីតដែលមានទម្រង់៖
`S_n=a_1b_1+a_2b_2+a_3b_3+......+a_ab_n` ដែល `(a_n)` ជាស្វ៉ីតនពន្តមានផលសងរួម d និង `( b_n)` ជាស្វ៉ីតធរណីមាត្ររេសុង q ។ ដើម្បីគណនាផលបូកនេះគេត្រូវគណនា `S_n-qS_n` រួចទាញរក `S_n` ។
៧. សំគាល់
គេឲ្យ `S_n=sum_{k=1}^n (u_k)=u_1+u_2+u_3+...+u_n`
ដើម្បីគណនាផលបូកខាងលើនេះគេត្រូវ៖
-
សរសេរតូ `u_k` ជារាង `u_n=t_(k+1)-t_k` ឬ `u_n=t_k-t_(k+1)` (បើអាច)
-
ករណីគេអាចសរសេរ `u_k=t_(k+1)-t_k` នោះគេបាន៖
`S_n=sum_{k=1}^n (u_k)=sum_{k=1}^n(t_(k+1)-t_k)=t_(k+1)-t_1`
-
ករណីគេអាចសរសេរ `u_k=t_k-t_(k+1)` នោះគេបាន៖
`S_n = sum_{k=1}^n (u_k) = sum_{k=1}^n (t_k-t_(k+1)) = t_1 = t_(n+1)`
III. របៀបកំណត់តួទី n តាមផលសងតួនៃស្វ៉ីត
១. ផលសងតួសំដាប់ទីមួយ៖
គេមានស្វ៉ីត `(a_n):a_1;a_2;a_3;....;a_n` ហើយ `b_1=a_2-a_1; b_2=a_3-a_2; b_3=a_4-a_3;....`
នោះគេថាស្វ៉ីត `(b_n):b_1;b_2;b_3;....;b_n` ជាផលសងតួលំដាប់ទីមួយនៃស្វ៉ីត `(a_n)`។
រូបមន្តគណនាតួ `a_n`
គេមាន `b_n=a_(n+1)-a_n`
គេមាន `sum_{k=1}^(n-1) (b_k) = sum_{k=1}^n-1 (a_(k + 1) - a_k)`
ដោយ `sum_{k=1}^(n-1) (a_(k+1) - a_k) = (a_2 - a_1) + (a_3 - a_2) +...+(a_n - a_(n -1)) = a_n - a_1`
គេបាន `sum_{k=1}^(n-1) (b_k) = a_n -a_1`
ដូចនោះ គេបាន `a_n = a_1 + sum_{k -1}^(n-1) (b_k)` ។
២. ផលសងតួសំដាប់ទីពី៖
គេមានស្វ៉ីត `(a_n):a_1;a_2;a_3;....;a_n` ហើយ` b_1=a_2-a_1; b_2=a_3-a_2; b_3=a_4-a_3;....;b_n=a_(n+1)-a_n` នោះគេថាស្វ៉ីត `(b_n):b_1;b_2;b_3;....;b_n` ជាផលសងតួលំដាប់ទីមួយនៃស្វ៉ីត `(a_n)`។
រូបមន្តគណនាតួ `a_n` គឺ `a_n = a_1 + sum_{k=1}^(n-1) (b_k)` ។
ស្វ៉ីត `(c_n)` ជាផលសងដំដាប់ទីពីរនៃស្វ៉ីត `(a_n)` គឺជាផលសងលំដាប់ទីមួយនៃស្វ៉ីត `(b_n)` ដែល `c_n=b_(n+1)-b_n ; n= 1, 2, 3, ....`
រូបមន្តគណនាតួទី n គឺ `b_n=c_1+ sum_{i=1}^(n-1) (c_i) ; n ge 2 `។
III. របៀបកំណត់តួទី n តាមផលសងតួនៃស្វ៉ីត
និយមន័យ៖
P(n) ជាសំណើដែលទាក់ទងនឹងចំនួនគត់ n ដើម្បីស្រាយបញ្ញាក់ថា P(n) ពិតចំពោះគ្រប់ nIN* គេត្រូវ៖
ផ្ទៀតផ្ទាត់ថា P(n) ពិតចំពោះ n=1
ឧបមាថា P(n) ពិតចំពោះតម្លៃ n
ស្រាយបញ្ញាក់ថា P(n) ពិតនាំឲ្យបាន P(n+1)ពិត
IV. របៀបគណនាទូទៅនៃស្វ៉ីតតាមទំនាក់ទំនងកំណើន
១. ករណីស្គាល់ទំនាក់ទំនងកំណើន `u_(n+1)=au_n+b`
បើគេស្គាល់ថា (`u_n`) ជាស្វ៉ីតនៃចំនួនពិតហើយផ្ទៀងផ្ទាត់ទំនាក់ទំនងកំណើត `u_(n+1)=au_n+b`ចំពោះគ្រប់ `nin IN`* និងមានតួ `u_1=alpha(|a| ne 1, a ne 0)` ។ ដើម្បីកំណត់រកតួ `u_n` គេត្រូវពិចារណាដូចខាងក្រោម៖
រកឬសសមីការ r=ar+b (ហៅថាសមីការសំគាល់នៃស្វ៉ីត)
តាងស្វ៉ីតជំនួយ `v_n=u_n-r` រួចត្រូវង្ហាញថា (`v_n`) ជាស្វ៉ីតធរណីមាត្រ។
រកឲ្យឃើញនូវតួ `v_n` បន្ទាប់មកគេទាញ `u_n=v_n+r` ។
២. ករណីស្គាល់ទំនាក់ទំនងកំណើន `u_(n+2)=au_(n+1)+bu_n`
បើគេស្គាល់ថា (`u_n`) ជាស្វ៉ីតនៃចំនួនពិតហើយផ្ទៀងផ្ទាត់ទំនាក់ទំនងកំណើន `u_(n+2)=au_(n+1)+bu_n` ចំពោះគ្រប់ `n in IN`* និងមានតួ `u1 = alpha ` , `u2 = beta`។ ដើម្បីកំណត់រកតួ `u_n` គេត្រូវពិចារណាសមីការ`r^2=ar+b` ឬ `(E): r^2-a.r-b`=0 (ហៅថាសមីការសំគាល់នៃស្វ៉ីត) គេត្រូវសិក្សាករណីផ្សេងៗដូចខាងក្រោម៖
បើ`Delta =a^2+4b > 0` សមីការសំគាល់(E) មានឬសពីរផ្សេងគ្នាជាចំនួនពិត `r^1` និង `r^2`។
ក្នុងករណីនេះដើម្បីគណា un យើងត្រូវអនុវត្តន៍ដូចខាងក្រោម៖
តាងស្វ៉ីតជំនួយពីរគឺ `x_n=u_(n+1)-r_1u_n` និង `y_n=u_(n+1)-r_2u_n`
រកប្រភេទនៃស្វ៉ីត (`x_n`) និង (`y_n`) រួចគណនា `x_n` និង `y_n` ជាអនុគមន៍នៃ n ។ ឧបមាថាគេបាន `x_n=f(n)` និង `y_n=g(n)`
យើងបានប្រព័ន្ធសមីការ `u_(n+1)-r_1u_n=f(n)` ; `u_(n+1)-r_2u_n=g(n)`
ដោះស្រាយរក `u_n` គេទទួលបាន `u_n=(f(n)-g(n))/(r_2-r_1)` ។
បើ ` Delta =a^2+4b=0` សមីការសំគាល់(E) មានឬសពីឌុប `r_1=r_2=r_0`។ ក្នុងករណីនេះដើម្បីគណនា `u_n` យើងត្រូវអនុវត្តន៍ដូចខាងក្រោម៖
តាងស្វ៉ីតជំនួយ `v_n=u_(n+1)-r_0u_n` រួចរកប្រភេទនៃស្វ៉ីត (`v_n`) និងគណនា `v_n` ជាអនុគមន៍នៃ n ។ ឧបមាថា `v_n=f(n)`។
គេទាញបានសមីការ `u_(n+1)-r_0u_n=f(n)` រួចត្រូវបំលែងជាទម្រង់៖ `(u_(n+1))/(r_0^(n+1))-u_n/r_0^n=f(n)/(r_0^(n+1))` (ចែកសមីការនឹង `r_0^(n+1)`)
ទាញឲ្យបាន `u_n = r_0^n [ u_1/r_0 + sum_{k=1}^(n-1) [ f(k)/(r_0^(k+1))] ]`
បើ `Delta =a^2+4b <` 0 សមីការសំគាល់(E) មានឬសពីរជាចំនួនកុំផ្លិចឆ្នាស់គ្នាគឺ `r_1=p+i.q , r_2=p-i.q , p,q in IR`។ ។ ក្នុងករណីនេះដើម្បីគណនា `u_n` យើងត្រូវអនុវត្តន៍ដូចខាងក្រោម៖
តាងស្វ៉ីតជំនួយ `Z_n=u_(n+1)-(p+i.q)u_n` រូចត្រូវស្រាយថា (`Z_n`) ជាស្វ៉ីតធរណីមាត្រនៃចំនួនកុំផ្លិច។ រួចគណនា `Z_n` ជាអនុគមន៍នៃ n ។
ឧបមាថា `Z_n=A_n+i.B_n ; A_n , B_n in IR , n in IN* `។
គេបានសមីការ `_(n+1)-(p+iq)u_n=A_(n+i).B_n`
ទាញឲ្យបានថា `u_n=-B_n/q` ។
៣. ករណីស្គាល់ទំនាក់ទំនងកំណើន `u_(n+2)=au_(n+1)+bu_n+c`
បើគេស្គាល់ថា (`u_n`) ជាស្វ៉ីតនៃចំនួនពិតហើយផ្ទៀងផ្ទាត់ទំនាក់ទំនងកំណើន `u_(n+2)=au_(n+1)+bu_n` ចំពោះគ្រប់ `n in IN`* និងមានតួ `u_1= alpha , u_2= beta`។ ដើម្បីកំណត់រកតួ `u_n` គេត្រូវអនុវត្តដូចខាងក្រោម៖
តាងស្វ៉ីតជំនួយ `w_n=u_n+ lambda`
គេបាន `u_n=w_n- lambda, u_(n+1)=w_(n+1)- lambda , u_(n+2)=w_(n+2)- lambda`
យក `u_n , u_(n+1) , u_(n+2)` ជំនួសក្នុង `u_(n+2)=au_(n+1)+bu_(n+1)+c` គេបានសមីការ៖`w_(n+2)- lambda =a(w_(n+1)- lambda)+b(w_n- lambda)+c` `w_(n+2)=aw_(n+1)+bw_n+(1-a-b) lambda+c`
ត្រូវឲ្យ `(1-a-b) lambda +c=0` គេទាញបាន `lambda =c/(a+b-q)` (ដែល `a+b ne 1`)
ក្នុងករណីនេះគេបានទំនាក់ទំនងកំណើន `w_(n+2)=aw_(n+1)+bw_n`
ដោះស្រាយរកតួ `w_n` តាមវិធីសាស្រ្តដែលបានសិក្សារួចហើយខាងលើបន្ទាប់មកទាញរកតួ `u_n=w_n-lambda=w_n-c/(a+b-q)`
អនុគមន៍ត្រីកោណមាត្រ
១. ទំនាក់ទំនងគ្រឹះ
`sin^2 theta+cos^2 theta = 1`
`tan theta =sin theta/cos theta`
`cot theta=cos theta /sin theta`
`tan.cot theta=1`
`1+tan^2 theta=1/cos^2 theta`
`1+cot^2 theta=1/sin^2 theta`
២ រូបមន្តផលបូក និងផលដក
`sin(a+b)=sin a cos b- sin b cos a`
`cos(a+b)=cos a cos b- sin a sin b`
`tan(a+b)=(tan a + tan b)/(1-tan a tan b)`
`sin(a-b)=sin a cos b- sin b cos a`
`cos(a+b)=cos a cos b+ sin a sin b`
`tan(a-b)=(tan a - tan b)/(1+tan a tan b)`
៣ រូបមន្តមុំឌុច
`sin2a=2sin a cos a`
`cos2a=cos^2a-sin^2a=2cos^2a-1=1-sin^2a`
`tan2a=2tan/(1-tan2a)`
`cot2a=cot^2a-1/(2cot a)`
៤ រូបមន្តកន្លះមុំ
`sin^2a/2=(1-cos a)/2`
`cos^2a/2=(1+cos a)/2`
`tan^2a/2=(1-cos a)/(1+cos a)`
៥ កន្សោម sin x, cos x, tan x ជាអនុគមន៍នៃ `t=tanx/2`
`sin x=2t/(1+t^2)`
`cos x=(1-t^2)/(1+t^2)`
`tan x=(1-t^2)/(1+t^2)`
៦ កន្សោម sin3a, cos3a, tan3a
`sin3a=3sin a-4sin^3 a`
`cos3a=4cos^3 a-3cos a`
`tan3a=(3tan a-tan^3 a)/(1-3tan^2 a)`
៧ រូបមន្តបំលែងពីផលគុណទៅផលបូក
`cos a cos b=1/2[cos(a+b)+cos(a-b)]`
`sin a sin b=1/2[cos(a-b)-cos(a+b)]`
`sin a cos b=1/2[sin(a+b)+sin(a-b)]`
`sin b cos a=1/2[sin(a+b)-sin(a-b)]`
៨ រូបមន្តបំលែងពីផលបូកទៅផលគុណ
`cos p +cos q=2cos((p+q)/2)cos((p-q)/2)`
`cos p -cos q=2sin((p+q)/2)sin((p-q)/2)`
`sin p+sin q=2sin((p+q)/2)cos((p-q)/2)`
`sin p-sin q=2sin((p-q)/2)cos((p+q)/2)`
`tan p+tan q=(sin(p+q))/(cos p cos q)`
`tan p-tan q=(sin(p-q))/(cos p cos q)`
`cot p+cot q=(sin(p+q))/(sin p sin q)`
`cot p-cot q=(sin(p-q))/(sin p sin q)`
៩ សមីការត្រីកោណមាត្រ
១. សមីការ sin u = sin v មានចម្លើយ
`{(u=v+2kpi,),(u=pi-v+2kpi, k in mathbb{Z}):}`
២. សមីការ cos u = cos v មានចម្លើយ
`{(u=v+2kpi,),(u= -v+2kpi, k in mathbb{Z}):}`
៣. សមីការ tan u = tan v មានចម្លើយ `u=v+kpi`
១០ រួបមន្តបម្លែងឆ្នូដែលគួកត់សំគាល់
`{(sin(pi/2-theta) = costheta),(cos(pi/2 - theta)= sintheta),(tan(pi/2 - theta) =cottheta):}`
`{(sin(pi-theta) = sintheta),(cos(pi - theta)= - costheta),(tan(pi - theta) = - tantheta):}`
`{(sin(pi/2+theta) = costheta),(cos(pi/2 - theta)= -sintheta),(tan(pi/2 - theta) = -cottheta):}`
`{(sin(pi+ theta) = -sintheta),(cos(pi + theta)= -costheta),(tan(pi + theta) = tantheta):}`
`{(sin(theta + 2kpi) = sintheta),(cos(theta + 2kpi)=costheta),(tan(theta + kpi) =tantheta):}`
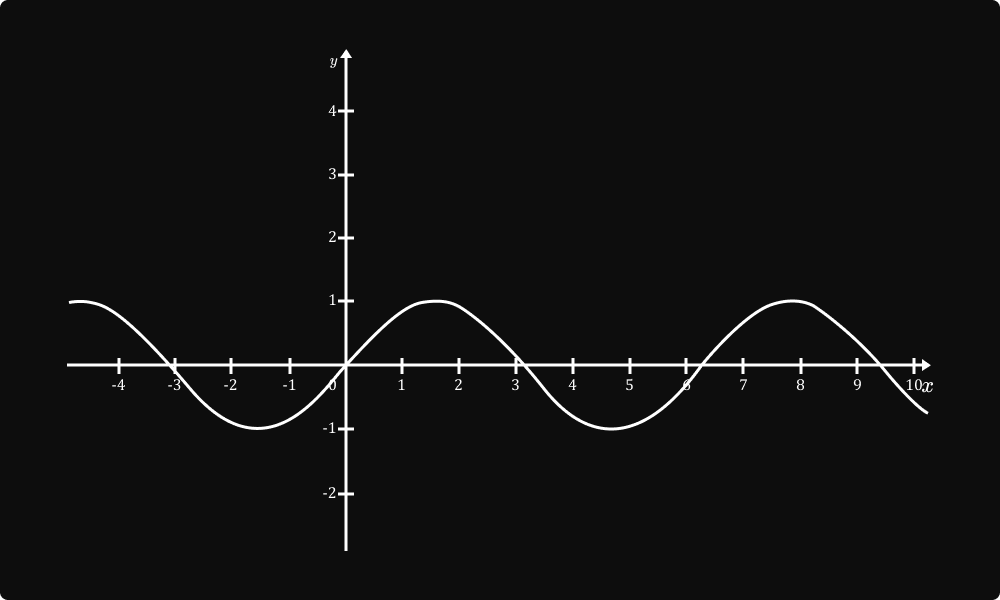
១១ ក្រាហ្វិកអនុគមន៍ត្រីកោណមាត្រ
១. ខ្សែកោងអនុគមន៍ y=sin x
២. ខ្សែកោងអនុគមន៍ y=cos x
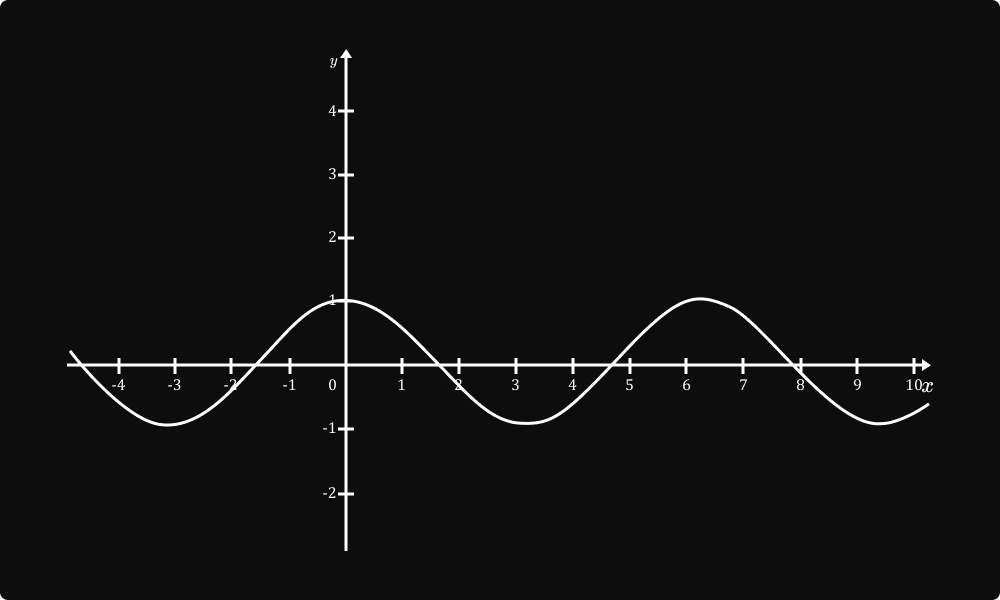
៣. ខ្សែកោងអនុគមន៍ y=tan x
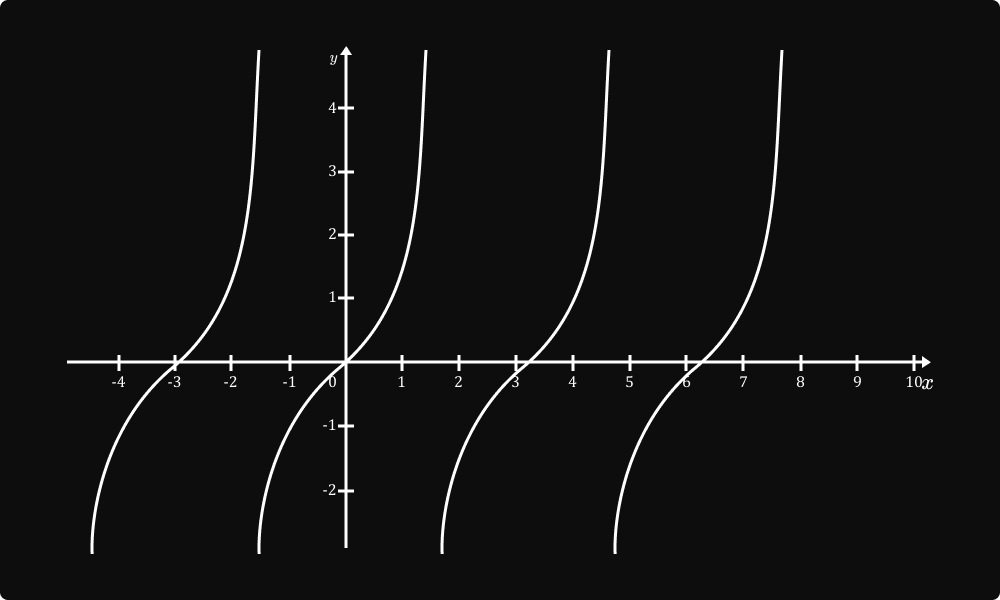
៣. ខ្សែកោងអនុគមន៍ y=cot x
អនុគមន៍អិចស៉្បូណង់ស្យែល និង អនុគមន៍លោការីត
១.អនុគមន៍អិចស៉្សូណង់ស្យែល
អនុគមន៍អិចស៉្បូណង់ស្យែល ជាអនុគមន៍កំណត់ដោយ `y=f(x)=a^x` ដែល `x in mathbb{R}` និង a ជាចំនួនពិតវិជ្ជមាន និងខុសពី 1។
ក្រាបនៃអនុគមន៍អិចស៉្បូណង់ស្យែល
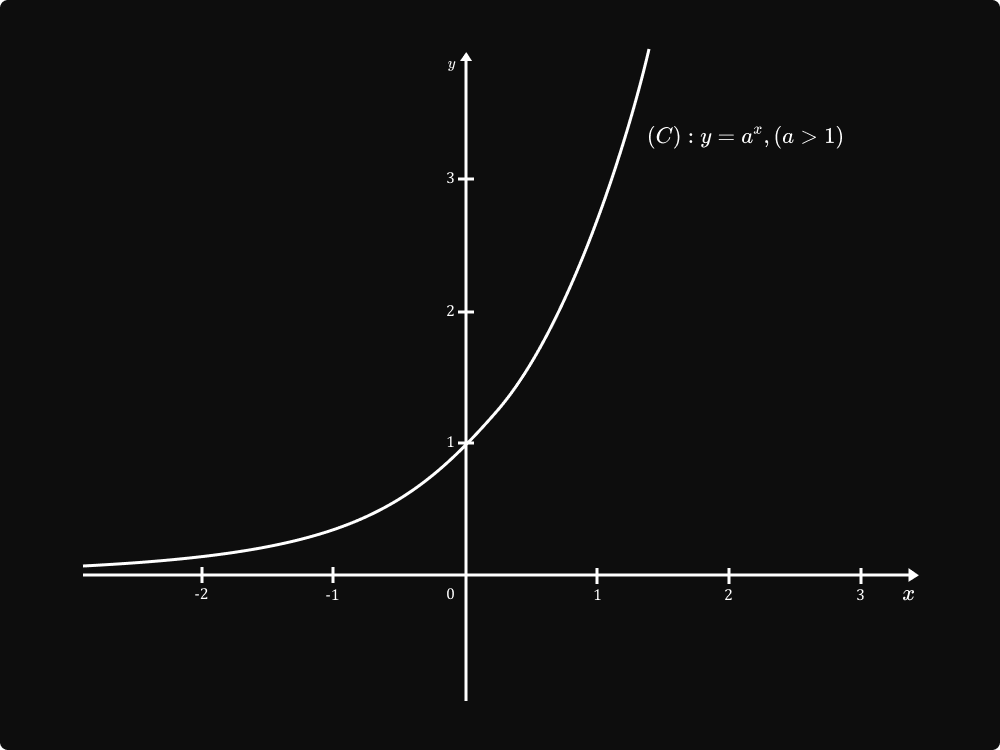
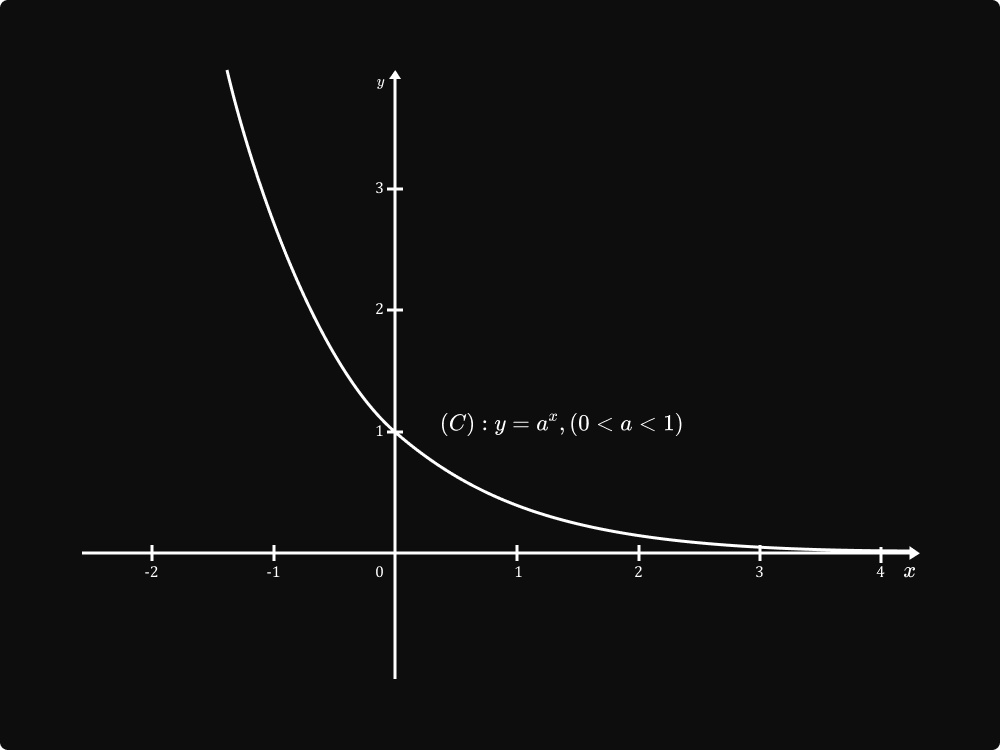
ចំពោះគ្រប់ចំនួនពិត a > 1 និង `a ne 1` គេបាន
`a^x = a^k Leftrightarrow x = k`
`a^f(x) = a^g(x) Leftrightarrow f(x) = g(x)`
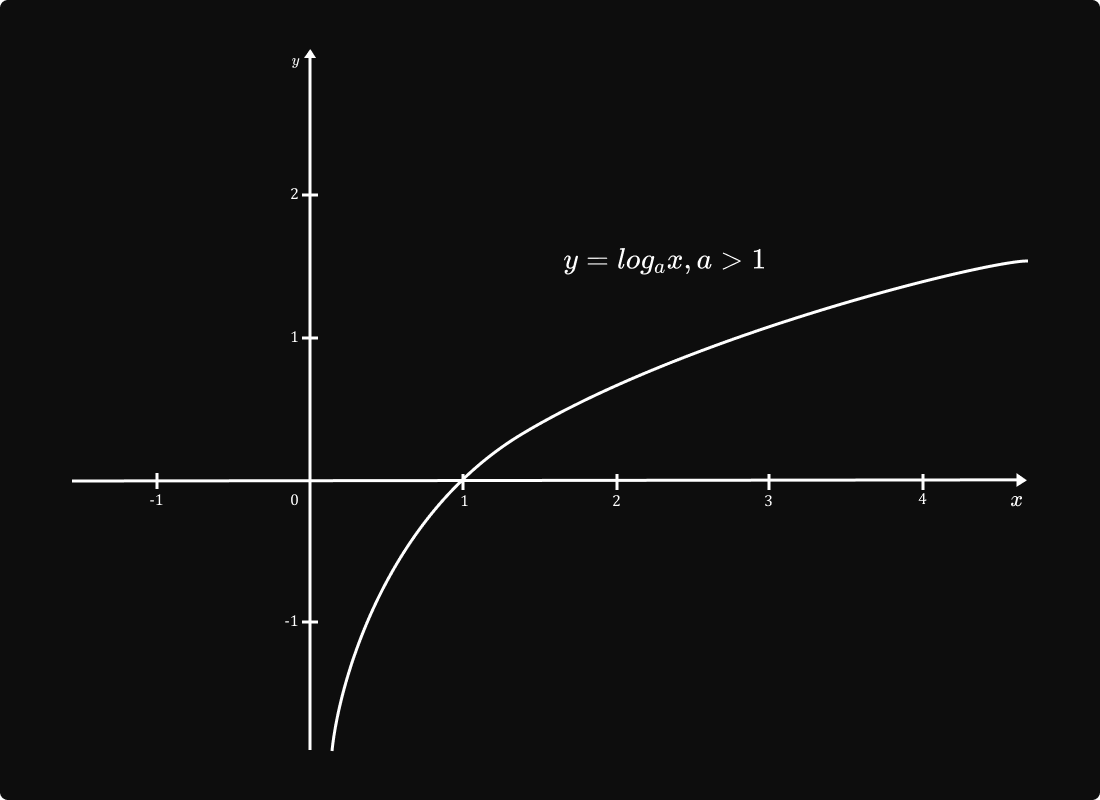
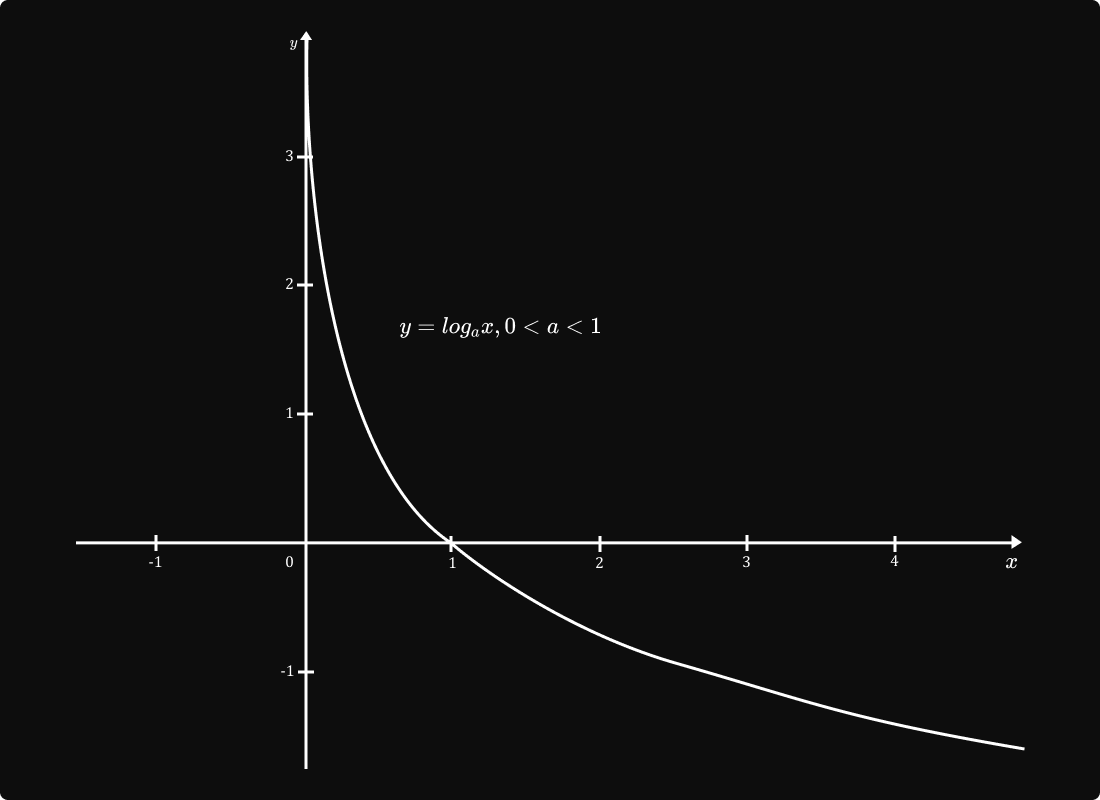
២.អនុគមន៍លោការីត
បើគេមាន `y=a^x` នោះ `x=log_ay` ដែល y > 0 , a > 0 និង `a ne 1` ។ គេថា `f(x)=a^x` មានអនុគមន៍ច្រាស់ `f^-1(x)=log_ax` ។ ដូចនេះ `y=log_ax` ហៅថាអនុគមន៍លោការីតនៃ x មានគោល a ។
លក្ខណះនៃលោការីត គ្រប់ចំនួនពិតវិជ្ជមាន x និង y , a > 0 , a1 គេមាន៖
`log_a(xy)=log_ax+log_ay`
`log_a(x/y)=log_ax-log_ay`
`log_ax^n=nlog_ax`
`log_ax=1/log_xa`
`log_aa=1`
`log_a1`=0
`a^(log_ab)=b`
ក្រាបនៃអនុគមន៍លោការីត
លីមីត និង ភាពជាប់នៃអនុគមន៍
១. ប្រមាណវីធីលើលីមីត
| បើ `lim_(xrightarrowa) f(x)` | L | L `ne` 0 | L `ne` 0 | 0 | 0 | + `infty` | + `infty` | + `infty` |
| បើ `lim_(xrightarrowa) g(x)` | M `ne ` 0 | 0 | `pm infty` | `pm infty` | 0 | + `infty` | - `infty` | - `infty` |
| បើ `lim_(xrightarrowa) (f(x) + g(x))` | L + M | L | `pm infty` | `pm infty` | 0 | + `infty` | ? | - `infty` |
| បើ `lim_(xrightarrowa) (f(x)- g(x))` | L - M | L | `pm infty` | `pm infty` | 0 | ? | + `infty` | ? |
| បើ `lim_(xrightarrowa) (f(x) cdot g(x))` | L `cdot` M | 0 | `pm infty` | ? | 0 | + `infty` | - `infty` | + `infty` |
| បើ `lim_(xrightarrowa) f(x)/g(x)` | `L/M` | `pm infty` | 0 | 0 | ? | ? | ? | ? |
កំណត់សម្គាល់៖ រាងមិនកំណត់គឺ៖ ` ltlt infty - infty gtgt ; ltlt infty times 0gtgt; ltlt 0/0 gtgt;ltlt infty/infty gtgt `
២. លីមីតនៃអនុគមន៍បណ្តាក់
និយមន័យ៖ យើងមាន u ជាអនុគមន៍កំណត់លើ I និង g ជាអនុគមន៍កំណត់លើ u(I) ។
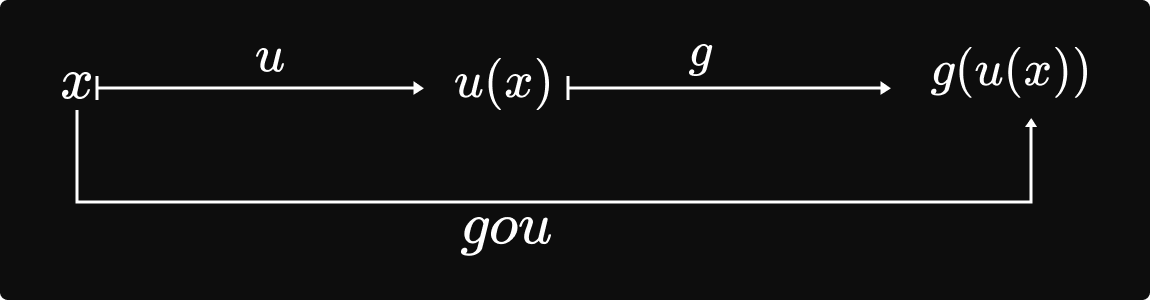
អនុគមន៍បណ្តាក់នៃ u ដោយ g គេសរសេរ g `circ` u ជាអនុគមន៍កំណត់លើ I ដោយ `(g circ u)(x)=g(u(x))` ។ បើ u និង g ជាអនុគមន៍ដែលមាន`lim_(xrightarrowalpha)u(x)= beta` និង `lim_(xrightarrowalpha)g(x)= gamma` នោះ `lim_(xrightarrowalpha)(g circ u)(x)= gamma`។
៣. លីមីតតាមការប្រៀបធៀប
-
បើ `f(x) ge g(x)` និង បើ `lim_(xrightarrow+infty)g(x)=+infty `នោះ `lim_(xrightarrow+infty)f(x)=+infty`
-
បើ `f(x) le g(x)` និង បើ `lim_(xrightarrow+infty)g(x)= - infty `នោះ `lim_(xrightarrow+infty)f(x)=- infty`
-
បើ `h(x)le f(x) le g(x)` និង បើ `lim_(xrightarrow+infty)h(x)=L` នឹង `lim_(xrightarrow+infty)g(x)=L `នោះ `lim_(xrightarrow+infty)f(x)=L`
-
បើ `|f(x)-L| le g(x)` និង បើ `lim_(xrightarrow+infty)g(x)=`0 នោះ `lim_(xrightarrow+infty)f(x)=L`
កំណត់សម្គាល់៖ គេអាចបកស្រាយដូចគ្នាកាលណា `x rightarrow - infty` ឬកាលណា `x rightarrow a ` (a ជាចំនួនពិត)
៤. លីមីតនៃអនុគមន៍ជួបប្រទះញឹកញាប់
លីមីតត្រង់ ` + infty: lim_(x rightarrow + infty) x^n = + infty; lim_(x rightarrow infty) sqrtx = + infty ; lim_(x Rightarrow infty) 1/x^n`=0
លីមីតត្រង់ 0 :
- n ជាចំនូនគត់រឺឡាទីបវិជ្ជមាន និងគូ `lim_(x rightarrow 0)1/x^n = + infty` ,x > 0
- n ជាចំនូនគត់រឺឡាទីបវិជ្ជមាន និងសេស `lim_(x rightarrow 0) 1/x^n = - infty` ,x < 0
- n ជាចំនូនគត់រឺឡាទីបវិជ្ជមាន និងសេស `lim_(x rightarrow 0) 1/x^n = + infty` ,x > 0
៥. លីមីតនៃអនុគមន៍ត្រីកោណមាត្រ
`lim_(x rightarrow 0)(sinx/x) = 1`; `lim_(x rightarrow 0)((1-cosx)/x) = 0`
៦. លីមីតនៃអនុគមន៍លោការីតនេពែ
`lim_(x rightarrow + infty) ln x = + infty; lim_(x rightarrow 0^+) ln x = - infty; lim_(x rightarrow + infty) (ln x )/x =` 0; ` lim_(x rightarrow + infty)xlnx = 0; lim_(x rightarrow 0^+) lnx/x = - infty; `
បើ n > 0 នោះ `lim_(x rightarrow + infty) lnx/x^n = 0 ; lim_(x rightarrow 0^+) x^nlnx = `0
ដេរីវេ និង ពី្រមីទីវនៃអនុគមន៍
១. ដេរីវេនៃអនុគមន៍
ក. រូបមន្តលើដេរីវេ
| ដែនកំណត់នៃអនុគមន៍ | f(x) | f'(x) |
| `Df=Df'= mathbb{R}` | a | 0 |
| ax + b | a | |
| `ax^2` + bx + c | 2ax + b | |
| `x^n(n in mathbb{R})` | `nx^(n-1)` | |
| `Df=Df'= mathbb{R}^*` | `1/x` | `-1/x^2` |
| `D_f = D_f' = mathbb{R}^*` | `sqrtx` | `1/(2sqrtx)` |
| លក្ខខណ្ឌ | អនុគមន៍ | អនុគមន៍មានដេរីវេកំណត់លើចន្លោះ `I` |
| អនុគមន៍ u និង v មានដេរីវេ នៅលើចន្លោះ `I` និង `lambda` ចំនួនថេរ | u + v | u' + v' |
| u.v | u'v + u.v' | |
| `lambda`u | `lambda`v | |
| អនុគមន៍ u និង v មានដេរីវេ នៅលើចន្លោះ `I` និង v ` ne ` 0 លើ `I` | `1/v` | `-v^1 / v^2` |
| `u/v` | `(u'.v-u.v')/v^2` | |
| អនុគមន៍បណ្តាក់ u មានដេរីវេលើ `I`, v មានដេរីវេលើ u (`I`) | `v circ u` | `(v' circ u) times u'` |
| u មានដេរីវេលើ `I`, u > 0 លើ`I` | `sqrty` | `(u')/(2sqrtu)` |
| `u^n (n in mathbb{R})` | n`u^(n-1).u'` |
ខ. ដេរីវេ នៃអនុគមន៍ត្រីកោណមាត្រ
| ដែនកំណត់ | f(x) | f'(x) |
| `Df=Df'= mathbb{R}` | cosx | - sinx |
| sinx | cosx | |
| `D_f=D_f'- mathbb{R} = { pi/2 + kpi, kinmathbb{Z}}` | tanx | `1 - tan^2 x = 1/cos^2 x ` |
| sinu | u'cosu | |
| cosu | `-u'sinu` | |
| tanu | `u'(1+tan^2 u) = u'/cos^2 u` | |
| cotu | `-u'(1+cot^2 u) =( u')/sin^2 u` |
បើ f(x)មានដេរីវេបន្តបន្ទាប់រហូតដល់លំដាប់ n យើងកំណត់តាងដោយ `f^(n) (x)`ដែល `f^(n) (x)=[f^(n-1) (x)]'`។
គ. ដេរីវេ នៃអនុគមន៍អ៉ិចស្បូណង់ស្យែល និង លោការីតនេពែ
| ដែនកំណត់ | f(x) | f'(x) |
| `Df=Df'= mathbb{R}` | `e^x` | `e^x` |
| `e^u` | `u'e^u` | |
| `D_f=[0,+infty ]` | ln x | `1/x ` |
| ln u | `(u')/u` |
ឃ. ដេរីវេ នៃអនុគមន៍អ៉ិចស្បូណង់ស្យែល និង លោការីតនេពែ
ល្បឿននៃចលនាមួយនៅខណ t គឺ v(t)=`(ds)/dt`=s'(t) ដែល s(t) ជាចម្ងាយចរនៅខណ t ។
សំទុះនៃចលនាមួយនៅខណ t គឺ a(t)=`(dv)/dt`=v'(t) ដែល v(t) ជាចម្ងាយចរនៅខណ t ។
២. ព្រីមីទីវនៃអនុគមន៍
ក. ព្រីមីទីវនៃអនុគមន៍ជូបប្រទះញឹកញាប់ (k ជាចំនួនថេរ)
| អនុគមន៍f(x) | ពី្រមីទីវF(x) |
| f(x)=0 | F(x)=k |
| f(x)=a | F(x)=ax+b |
| `f(x)=x^n (n ne -1)` | `F(x)=x^(n+1)/(n+1) +k ` |
| ln u | `(u')/u` |
| f(x)= `1/sqrtx` | `F(x) = 2 sqrtx + k` |
| f(x)= `1/sqrtx^2` | `F(x) = -1/((n-1)x^(n-1)) +k` |
| f(x)= `1/x^2 (n ge 2)` | `F(x) = 2 sqrtx + k` |
| f(x)= `1/x` | `F(x) = ln|x| + k` |
| f(x)= `sinx` | `F(x) = - cos x + k` |
| f(x)= `cosx` | `F(x) = sin x +k` |
| a`ne`0, f(x)=cos(ax+b) | `F(x)=1/a sin(ax+b)+k` |
| a`ne`0, f(x)=cos(ax+b) | `F(x)= - 1/a cos(ax+b)+k` |
| f(x)=` 1/cos^2x`=1+`tan^2 x` | `F(x)=tan x+k` |
| f(x)=`- 1/sin^2x`=1+`cot^2 x` | `F(x)= - cosx + k` |
| f(x)=`e^x` | `F(x)= e^x + k` |
ខ.ប្រមាណវិធីលើព្រីមីទីវ (c ជាចំនួនថេរ)
| អនុគមន៍ | ពី្រមីទីវ |
| f+g | F+G+c |
| `lambda f` | `lambda f + c` |
| u'v+uv' | uv+c |
| `(u'v-uv')/v^2` | `u/v`+c |
| (v'`circ ` u) `times` u' | v' `circ u +c` |
| `u^n u'` | `u^(n+1)/(n+1) + c` |
| `(u')/u^n (n ne 1)` | `- 1/((n-1)u^(n-1))` |
| `(u')/sqrtu` | `2sqrtu` |
អាំងតេក្រាល
មេរៀនសង្ខេប
-
អនុគមន៍ ` f ` មានព្រីមីទីវ F លើចន្លោះ `I` និង a និង b ជាធាតុរបស់ `I` នោះ
`int_a^b f(x) dx = [F(x)]_a^b = F(b) - F(a)`
-
`int_a^b f(x) dx = `0
-
អនុគមន៍ `f` មានព្រីមីទីវ `I`និង a និង b ជាធាតុរបស់ `I` នោះ `int_a^b f(x)dx = - int_a^b f(x)`
-
អនុគមន៍ `f` មានព្រីមីទីវ `I` ។ គ្រប់ a, b, c ធាតុរបស់ `I` (a < b < c)
`int_a^b f(x) dx + int_b^c f(x) dx = int_a^c f(x) dx`
-
អនុគមន៍ `f` និង `g` មានព្រីមីទីវ `I` ។ គ្រប់ a, b របស់`I` និង គ្រប់ `lambda` នៃ `mathbb{R}`
`int_a^b[f(x) + g(x)]dx = int_a^b f(x) + int_a^bg(x)dx `
`int_a^b lambdaf(x)dx = int_a^b f(x)dx`
-
អនុគមន៍ `f` និង `g` ជាអនុគមន៍ជាប់លើ `I` និងមានដេរីវេលើ `I` និង a, b ជាធាតុរបស់ `I`
`int_a^b f(x)g'(x)dx = [f(x)g(x)]_a^b = int_a^bf'(x)g(x)dx`
សមីការឌីផេរ៉ង់ស្យែល
1.សមីការឌីផេរ៉ង់ស្យែលលំដាប់ទី1
និយមន័យ : សមីការឌីផេរ៉ង់ស្យែលលីនេអ៊ែលំដាប់ទី 1 មេគុណថេរអូម៉ូសែន ( អង្គទី 2 ស្មើសូន្យ ) ជាសមីការដែលមានរាងទូទៅ y'+ay=0 (a ជាចំនួនថេរ)។
ចម្លើយទូទៅនៃសមីការគឺ `y =Ae^(-alphax)` ដែល A ជាចំនួនថេរណាមួយក៏បាន។
ដើម្បីដោះស្រាយសមីការឌីផេរ៉ង់ស្យែលលីនេអ៊ែលំដាប់ទី 1 មេគុណថេរ មិនអូម៉ូសែន y' + ay = p(x), p(x) ` ne ` 0 គេត្រូវ :
រកអនុគមន៍ចម្លើយទូទៅនៃសមីការ y'+ay=0 តាងដោយ `y_c`
រកអនុគមន៍ចម្លើយពិសេសនៃសមីការ y' + ay = p(x) តាងដោយ `y_p`
ចម្លើយទូទៅនៃសមីការ y' + y = p(x) គឺអនុគមន៍ y ដែល : `y = y_c + y_p` ។
វិធីបម្រែបម្រួលថេរ : ដើម្បីដោះស្រាយសមីការ y' + ay = p(x) (E), `p(x) ne 0`
នោះគេត្រូវ :
រកចម្លើយទូទៅនៃសមីការ y' +ay =0 គឺ y =`Ae^(- alpha x) ` ( A ជាចំនួនថេរណាមួយក៏បាន)
ក្នុងចម្លើយ y =`Ae^(- alpha x )` ជំនួសចំនួនថេរ A ដោយអនុគមន៍ A(x)
ពី y = `A(x)e^(- alpha x) ` ទាញរក y' រួចយក y និង y' ជំនួសក្នុងសមីការy' + ay = p(x) ដើម្បីទាញរក p (x) គេបាន
`y = A(x)e^(- alpha x) `
` y'= A'(x)e^(- alpha x) -aA(x) e^(- alpha x) `
`(E) : A'(x)e^(- alpha x) - aA(x)e^(- alpha x) +aA(x)e^(- alpha x) = p(x) `
` A'(x)e^(- alpha x) =p (x) `
` A'(x)= e^(- alpha x) =p (x) `
` A(x)=e^( alpha x) p (x)dx+C , C` ជាចំនួនថេរណាមួយក៏បាន
ដូច្នេះ `y = e^( - alpha x) [ int e ^(alpha x) p(x)lx + c ] `
ចម្លើយទូទៅនៃ `(E)`គឺ ` y =ce^( - alpha x) +e^(alpha x) int e^(alpha x) p(x)dx `
ដែល ` y_c=ce^( - alpha x)` និង `y_p= e^( - alpha x) int e^(alpha x) p (x) dx `។
2.សមីការឌីផេរ៉ង់ស្យែលលីនេអ៊ែលំដាប់ទី 2
និយមន័យ : សមីការឌីផេរ៉ង់ស្យែលលីនេអ៊ែលំដាប់ទី 2 អូម៉ូសែន និងមានមេគុណថេរ ជាសមីការដែលអាចសរសេជារាងទូទៅ ay''+by'+cy=0 ដែល a,b,c ជាចំនួនពិត និង a ` ne ` 0 ។
ដំណោះស្រាយសមីការឌីផេរ៉ង់ស្យែលលីនេអ៊ែលំដាប់ទី 2 អូម៉ូសែននិងមានមេគុណថេរ
ជាទូទៅ
-
សមីការឌីផេរ៉ង់ស្យែលលីនេអ៊ែលំដាបទី 2y" +by' + cy = 0 អាចសរសេរ ជាសមីការ(y' —`alpha` y)' – `beta`(y'— `alpha` y)=0 ដែល `alpha` និង `beta` ជាឬសនៃសមីការ សម្គាល់ `lambda^2 + b lambda + C = 0 ( lambda in C ) ` ។
-
សមីការសម្គាល់ `lamba^2 + b lambda + C = 0` នៃសមីការឌីផេរ៉ង់ស្យែល y" + by + cy =0 អាចមានឬស 2 ជាចំនួនពិតផ្សេងគ្នា ឬមានឬសឌុបជាចំនួនពិត ឬ មានឬស 2 ជាចំនួនកុំផ្លិច។
ជាទូទៅ
-
រកសមីការសម្គាល់ `lambda^2 + lambdab + C = 0` នៃសមីការឌីផេរ៉ង់ស្យែល y" + by + cy =0
-
បើសមីការសម្គាល់មានឬស 2 ជាចំនួនពិតផ្សេងគ្នា `lambda_1 = alpha ` និង `lambda_2 = beta` នោះ
សមីការ y" + by' + cy =0 មានចម្លើយទូទៅ `y = Ae^(alpha x ) + Be^(alpha x )` ដែល A និង B ជាចំនួនថេរណាមួយក៏បាន
` y_1= e^(alpha x ) , y_2 =e^(beta x ) ` ជាចម្លើយគោល។
ជាទូទៅ រកសមីការសម្គាល់ `lambda^2 + lambdab + C = 0` នៃសមីការឌីផេរ៉ង់ស្យែល y" + by + cy =0 មានឬសកុំផ្លិច `lambda_1 = alpha + ibeta` និង `lambda_1 = alpha - ibeta` នោះគេបានចម្លើយទូទៅនៃ សមីការឌីផេរ៉ង់ស្យែលនេះគឺ ` y = e^(alphax) (C cos beta x + D sin beta x ) ` ដែល C និង Dជាចំនួនថេរណាមួយក៏បាន។
របៀបដោះស្រាយសមីការឌីផេរ៉ង់ស្យែលលីនេអ៊ែលំដាប់ទី 2 មិនអូម៉ូសែន
`y'' + by' + cy = p(x), p(x) ne 0`
-
ស្វែងរកចម្លើយពិសេសមិនអូម៉ូសែន តាងដោយ `y_p` នៃសមីការ y" +by'+ cy = p(x) ដែល `y_p` មានទម្រង់ដូចអង្គទី 2 p(x)
-
រកចម្លើយទូទៅតាងដោយ `y_c` នៃសមីការលីនេអ៊ែលំដាប់ទី 2 អូម៉ូសែន y" + by' + cy =0
-
គេបានចម្លើយទូទៅនៃសមីការលីនេអ៊ែលំដាប់ទី 2 មិនអូម៉ូសែន ជាផលបូកនៃ `y_c` និង `y_p` គឺ `y= y_c+ y_p`។
វ៉ិចទ័រក្នុងលំហ
I. មេរៀនសង្ខេប
-
បើ `vec{ U }=U_1 vec{i} + U_2 vec{j} + U_3 vec{k}` និង `vec{ V }=V_1 vec{i} + V_2 vec{j} + V_3 vec{k}` ជាវ៉ិចទ័រក្នុងលំហ។
ផលគុណនៃវ៉ិចទ័រ `vec{ U }` និង `vec{ V }` គឺជាវ៉ិចទ័រកំណត់ដោយ
`vec{ U } times vec{ V }= (u_2v_3 - u_3v_2)vec{i} - (u_1v_3 - u_3v_1)vec{j} + (u_1v_2 - u_2v_1)vec{k}` ។
-
បើ `vec{U}, vec{V}` និង `vec{K}` ជាវ៉ិចទ័រនៅក្នុងលំហ និង c ជាចំនួនពិត នោះគេបាន :
ក.`vec{u} times vec{v} = - (vec{v} times vec{u})`
ខ. `vec{u} times (vec{v} + vec{w}) = (vec{u} times vec{v}) + (vec{u} times vec{w})`
គ. `c(vec{u} + vec{V}) = (cvec{u} times vec{v}) = (vec{u} times (cvec{v})) `
ឃ. ` vec{u} times vec{0} = vec{0} times vec{u} = vec{0}`
ង. `vec{u} times vec{u} = vec{0}` ច. `vec{u}.(vec{v} times vec{w}) = (vec{u} times vec{v}) vec{w}`
-
បើ `vec{u}` និង `vec{v}` ជាវ៉ិចទ័រមិនសូន្យនៅក្នុងលំហ និងតាង `theta` ជាមុំរវាង `vec{u}` និង `vec{v}`នោះគេបាន :
ក. `vec{u} times vec{v}` អរតូកូណាល់ទៅនឹង `vec{u}` ផង និង `vec{v}` ផង។
ខ. `|vec{u} times vec{v} | = |vec{u}| times |vec{v}| · sin theta`
គ. បើ ` vec{u} times vec{v} = 0 ` នោះ ` vec{u}` និង ` vec{v}` ជាវ៉ិទ័រកូលីនេអ៊ែនឹងគ្នា ។
ឃ. `|vec{u} times vec{v}| ` =ផ្ទៃក្រឡារបស់ប្រលេឡូក្រាមដែលសង់លើវ៉ិចទ័រ `vec{u}` និង `vec{v}` ។
ង.`frac{1}{2}|vec{u} times vec{v}|`= ផ្ទៃក្រឡារបស់ត្រីកោណដែលសង់លើវ៉ិចទ័រ `vec{u}` និង `vec{v}` ។
-
គេមានវ៉ិចទ័រ `vec{u} , vec{v}` និង `vec{w}` នៅក្នុងលំហ ។ ផលគុណចម្រុះនៃ `vec{u} , vec{v}` និង `vec{w}` តាមលំដាប់គឺជាចំនួនពិតដែល កំណត់ដោយ `vec{u} , (vec{v} times vec{w})`។
-
បើគេមានវ៉ិចទ័រ `vec{u} = u_1 vec{i} + u_2 vec{j} + u_3 vec{k} , vec{v} = v_1 vec{i} + v_2 vec{j} + v_3 vec{k}` និង ` vec{w} = w_1 vec{i} + w_2 vec{j} + w_3 vec{k}` នោះ `vec{u}. (vec{v} times vec{w}) =| (u_1, u_2, u_3), (v_1, v_2, v_3), (w_1, w_2, w_3) | `
-
v ជាមាឌរបស់ប្រលេពីប៉ែតដែលសង់លើវ៉ិចទ័រនិង `vec{u} , vec{v}` និង `vec{w}` គឺ `V = |vec{u} · (vec{v} times vec{w} )|` និង `w` ជាមាឌរបស់តេត្រាអ៊ែតគឺ : `W=frac{| vec{u} .( vec{v} times vec{w} )|}6` បានន័យថាយកមាឌរបស់ប្រលេពីប៉ែតចែកនឹង 6។
-
សមីការប៉ារ៉ាម៉ែតនៃបន្ទាត់ `L` កាត់តាមចំណុច `P(x_0, y_0, z_0)` ហើយស្របនឹងវ៉ិចទ័រ
`v = (a, b, c)` គឺ `x = x_0 + at, y = y_0+bt, z = z_0 + ct` ឬ `{(x_0 = z_0 + at ),(x_0 = z_0 + bt ;t in mathbb{R}),(x_0 = z_0 + ct):}`
-
សមីការឆ្លុះនៃបន្ទាត់ `L` គឺ :
`frac{x-x_0}a=frac{y-y_0}b=frac{z-z_0}c` ។
-
សមីការស្តង់ដានៃប្លង់ដែលកាតតាមចំណុច `P (x_0, y_0, z_0)` និងមានវ៉ិចទ័រណរម៉ាល់ `vec{n} = (a, b, c)` គឺ `a (x − x_0) + b(y − y_0) + c(z −z_0 ) = 0` ។
-
សមីការទូទៅនៃប្លង់គឺ :
` ax + by + cz + d = 0 ` (ដែល` d = −(ax_0 + by_0 + cz_0)` )។
-
មុំរវាងប្លង់ពីរគឺ :
` cos theta = frac{|vec{n_1}.vec{n_2}|}|vec{n_1}.vec{n_2}| `ដែល `vec{n_1}` និង `vec{n_2}` ជាវ៉ិចទ័រណរម៉ាល់នៃប្លង់ ។
-
ចម្ងាយរវាងចំណុច `P (x_1, y_1, z_1)` និង `Q(x_2, y_2, z_2)`នៅក្នុងលំហគឺ :
`d=sqrt((x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2)` ។
-
សមីការស្តង់ដានៃស្វ៊ែផ្ចិត:
`C ( x_0 ,y_0 , z_0 )`កាំ `r` គឺ `(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=r^2`
-
សមីការទូទៅនៃស្វ៊ែ :
`x^2+y^2+z^2-2x_0x-2y_0y-2z_0z+k=0,k=x_0^2+y_0^2+z_0^2-r^2`
-
ចម្ងាយពីចំណុច `Q `ទៅប្លង់ `alpha` ដែលចំណុច `Q ` មិននៅក្នុងប្លង់ `alpha` កំណត់ដោយ:
`D=frac{|Pvec{Q}.vec{n}|}|vec{n}|` ឬ `D=frac{|ax_0+by_0+cz_0+d|}sqrt(a^2+b^2+c^2)` ដែល `P` ជាចំណុចនៅក្នុងប្លង់ `vec{n}` ជាវុីទ័រណាម៉ាល់នៃប្លង់។
-
ចម្ងាយពីចំណុច `Q` ទៅបន្ទាត់ `L` ក្នុងលំហកំណត់ដោយ `D=frac{|Pvec{Q} times vec{u}|}|vec{u}|` វ៉ិចទ័រប្រាប់ទិសនៃបន្ទាត់ `L` និង `P` ជាចំណុចនៅលើបន្ទាត់ `L` ។
ចំនួនកុំផ្លិច
មេរៀនសង្ខេប
ក. ចំនួនកុំផ្លិចក្នុងទម្រង់ពិជគណិត
`to` ចំនួនកុំផ្លិច `z=a+bi` ហៅថាទម្រង់កុំពិជគណិតនៃចំនួនកុំផ្លិច។ `a` ហៅថាផ្នែកពិត ហើយ `b` ហៅថាផ្នែកនិមិត្ត ដែល `a` និង `b` ជាចុំនួនពិត និង `i^2=-1`។
`to` បើ `z_1=a_1+ib_1` និង `z_2=a_2+ib_2` នោះគេបាន
`z_1=z_2 iff (a_1=a_2)` និង `(b_1=b_2)`
`z_1+z_2=(a_1+a_2)+i(b_1+b_2)`
`z_1-z_2=(a_1-a_2)+i(b_1-b_2)`
`z_1z_2=(a_1a_2 - b_1b_2)+i(a_1b_2+b_1a_2)`
`z_1z_2 = frac{a_1-ib_1}(a_2-ib_2) = frac{(a_1+ib_1)(a_2-ib_2)}(a_2^2+b_2^2) = frac{a_1a_2+b_1b_2}(a_2^2 + b_2^2) + i frac{a_2b_1 + a_1b_2}(a_2^2+b_2^2)`
`to` ចំនួនកុំផ្លិចឆ្លាស់នៃចំនួនកុំផ្លិច `z=a+bi` តាងដោយ `barz=a-ib`
`to` ចំនួនកុំផ្លិចផ្ទុយនៃចំនួនកុំផ្លិច `z=a+bi` តាងដោយ `-z=a-ib`
ចំនួនកុំផ្លិចក្នុងប្លង់កុំផ្លិច `z=a+bi` តាងដោយ `M` មានកូអរដោនេ `(a, b)` ក្នុងតម្រុយអរតូណរមេ `(xoy)`។ ចំពោះ `z=a+bi` អាចតាងដោយវ៉ិចទ័រ ទរ័ `vec{OM}( a,b )` គេថា `vec{OM}` ជាវ៉ិចទ័ររូប ភាពនៃចំនួនកុំផ្លិច `z = a + bi` ។ចំណុចក្នុងតម្រុយតាងចំនួនកុំផ្លិចប្លង់ដែលប្រដាប់ដោយតម្រុយនេះហៅ ថាប្លង់កុំផ្លិច ។ អ័ក្ស `( x`'`o x )` ជាអ័ក្សផ្នែកពិត ហើយអ័ក្ស `( y`'`oy )` ហៅថាអ័ក្សផ្នែកនិមិត្ត ។ ផលបូកន ចំនួនកុំផ្លិចមានរូបភាពជាផលបូកវ៉ិចទ័រក្នុងប្លង់កុំផ្លិច ។
ខ.ចំនួនកុំផ្លិចក្នុងទម្រង់ត្រីកោណមាត្រ
-
បើគេមានចំនួនកុំផ្លិច `z = a + bi ` នោះម៉ូឌុលនៃ `z` តាងដោយ
`r = |z| =sqrt(a^2+b^2) `
-
បើ `Z` ជាចំនួនកុំផ្លិចនោះ `|z| = |z| = |-z|`
-
បើ `Z_1` និង `Z_2` ជាចំនួនកុំផ្លិចនោះគេបាន `|Z_1`'`Z_2| = |Z_1| · | Z_2|
frac{|Z_1|}|Z_2|=frac{|Z_1|}|Z_2| ; |Z_1+Z_2| le Z_1+Z_2 `
-
វ៉ិចទ័រ `(0x , 0M )` ជារូបភាពនៃចំនួនកុំផ្លិច `z` តាង `varphi ` ( ជាមុំតូចបំផុត `( OM , OM )`)
`varphi ` ហៅថាអាគុយម៉ង់នៃចំនួនកុំផ្លិច `Z` ។ ដើម្បីគណនាមុំ `varphi ` យើងត្រូវដោះស្រាយប្រព័ន្ធសមីការ:
`{(cos varphi = frac{a}(sqrt(a^2 + b^2)) = frac{a}r),(sin varphi = frac{b}(sqrt(a^2 + b^2)) = frac{b}r):}`
`z = r( cos varphi + i sin varphi )` ហៅថាទម្រង់ត្រីកោណមាត្រនៃចំនួនកុំផ្លិច `z = a +ib`
-
បើ `Z_1 = r_1( cos varphi_1 + i sin varphi_1 ) ` និង `z_2= r_2(cos varphi_2 + i sin varphi_2 )` នោះគេបាន
`Z_1Z_2= r_1r_2[cos(varphi_1+ varphi_2) + i sin(varphi_1+varphi_2)]`
`frac{Z_1}Z_2=frac{r_1}r_2[r(cosvarphi_1- varphi_2 ) + i sin ( varphi_1 - varphi_2 ) ] `
`z^n=[ r (cos alpha + i sinvarphi )]^n =r^n[cos( n varphi )] ; n` ជាចំនួនគត់រុឺឡាទីប
បម្លែងវិលជុំវិញគល់តម្រុយនៃប្លង់កុំផ្លិចជាទូទៅមានចំនួនកុំផ្លិច `z = cos varphi +i sin varphi` បើ `M`'`( Z`'`)` ជារូបភាពនៃ `M (z)` តាមបម្លែងវិលផ្ចិត `O (O` ជាគល់តម្រុយ) នឹងមុំ នោះ `z`'` = (cos alpha + i sin alpha ) z` ។
គ.ស្វ័យគុណ n និង ឬសទី n នៃចំនួនកុំផ្លិច
`(cos varphi + i sin varphi )^n = cos( n varphi ) + i sin( n varphi)` ( ទ្រឺស្កីបទដឺម័រ ) `(Moivre)`
-
- បើ `z = r(cos varphi+ i sin varphi)` ជាចំនួនកុំផ្លិចមិនសូន្យ ហើយ `n` ជាចំនួនគត់វិជ្ជមាន នោះ `Z` មាន `n` ឬសទី `n` គឺ `W_0 , W_1,W_2, ..., W_n - 1` កំណត់ដោយ`W_k=\rootn\r[cos( frac{varphi + 2kpi}n) +i sin(frac{varphi + 2kpi}n)]` ខ ដែល `k=0,1,2,...., ( n - 1 )`
ឃ. អនុវត្តន៍ចំនួនកុំផ្លិចក្នុងធរណីមាត្រ
-
ជាទូទៅ បើ `A(Z_1)` និង `B(Z_2)` ជារូបភាពនៃចំនួនកុំផ្លិច `Z_1` និង `Z_2` នោះចម្ងាយ `AB = | Z_2 — Z_1| = | Z_1 — Z_2|` ។
-
ជាទូទៅ បើគេមាន `z_1` និង `z_1` ជាចំនួនកុំផ្លិចដែលមានរូបភាពរៀងគ្នា `A(Z_1)` និង `B(Z_2)` ហើយ ចំណុច `P (z)` ជារូបភាពនៃចំនួនកុំផ្លិច `z` ដែល `P` ស្ថិតនៅលើ `AB` ហើយចែក `AB` តាមផលធៀប`m ; n` នោះគេបាន `z = frac{Z_1 + lambda Z_2}(1+ lambda)`ដែល ` lambda = frac{m}n` ។
-
ជាទូទៅបើ `A (z ) ,B ( z_1)` និង `C (z_2)` បង្តើតបានត្រីកោណ `A B C` នោះគេបាន `frac{AC}(AB) = frac{Z_2- Z}(Z_1- Z)` ហើយ `angle BAC= arg (frac{Z_2- Z}(Z_1-Z))`
វិភាគបន្សំ និង ប្រូបាប៊ីលីត
I.មេរៀនសង្ខេប
ព្រឹត្តិការណ៍ផលគុណនៃ `A` និង `B` ជាប្រសព្វនៃព្រឹត្តិការណ៍ `A` និងព្រឹត្តិការណ៍ `B` ។
ព្រឹត្តិការណ៍ផលបូកនៃ `A` និង `B` ជាប្រជុំនៃព្រឹត្តិការណ៍ `A` និងព្រឹត្តិការណ៍ `B` ។
ព្រឹត្តិការណ៍ `B` និងព្រឹត្តិការណ៍ `D` ជាព្រឹត្តិការណ៍មិនចុះសម្រុង កាលណាព្រឹត្តិការណ៍ ផលគុណនៃ `B` និង `D` ជាព្រឹត្តិការណ៍មិនអាចមាន `B cap D = emptyset `
ព្រឹត្តិការណ៍ 2 ជាព្រឹត្តិការណ៍ផ្ទុយគ្នា ឬជាព្រឹត្តិការណ៍បំពេញគ្នា កាលណាព្រឹត្តិការណ៍ផលគុណនៃព្រឹត្តិការណ៍
ទាំង 2 ជាព្រឹត្តិការណ៍មិនអាចមាន និងព្រឹត្តិការណ៍ផលបូកនៃព្រឹត្តិការណ៍ទាំង 2 ជាព្រឹត្តិការណ៍ប្រាកដ : `A cap barA = emptyset , A cup bar A= S`
គេបានព្រឹត្តិការណ៍ 2 ផ្ទុយគ្នាជាព្រឹត្តិការណ៍មិនចុះសម្រុង។
ប្រូបាបនៃព្រឹត្តិការណ៍មួយ ជាផលធៀបនៃចំនួនករណីស្រប និងចំនួនករណីអាច `P(A)` =`frac{`ចំនួនករណីស្រប `n(A)}(`ចំនួនករណីអាច` n(S))`
ប្រូបាបនៃលំហសំណាក `S` ស្មើនឹង `1: P (S) = 1`
ប្រូបាបនៃព្រឹត្តិការណ៍មិនអាចមានស្មើស្មើនឹង `0 : P ( emptyset) = 0`
-
ប្រូបាបនៃព្រឹត្តិការណ៍មួយក្នុងលំហសំណាកជាចំនួនដែលនៅចន្លោះ `[0,1]
0 le P(A) le 1 `
-
ប្រូបាបជាអនុវត្តន៍ ដែលកំណត់ពីលំហសំណាក `S` ទៅចន្លោះ `[0,1]`
`P : S → [0,1] `
-
ប្រូបាបនៃព្រឹត្តិការណ៍ផលគុណ `A` និង `B` គឺ :
`P(A cap B) = P(A) times P(B)` បើ `A` និង `B` មិនទាក់ទងគ្នា
`P(A cap B) = P(A) times P(B)` (ដែល `A` កើតមុន) បើ `A` និង `B` ទំទាក់ទងគ្នា
-
ប្រូបាបនៃព្រឹត្តិការណ៍ផលបូក `A` និង `B` គឺ `P(A cup B) = P(A) + P(B) - P(A cap B)
P(A cup B) = P(A) + P(B)` បើ `A` និង `B` ជាព្រឹត្តិការណ៍មិនចុះសម្រុង
-
ប្រូបាបនៃព្រឹត្តិការណ៍ផ្ទុយ `A` គឺ:` P(bar A ) = 1 - P(A)`
-
បើ `A` និង `B` ជាព្រឹត្តិការណ៍ 2 ក្នុងលំហសំណាកមួយដែល `cup P(A) ne 0 `
នោះប្រូបាបមានលក្ខខណ្ឌនៃ
ព្រឹត្តិការណ៍ `B` ដោយដឹងថា `A` គឺ: `P (B|A) = frac{p ( A cap B )}(P(A))`
-
គេអាចគណនាបានដូចគ្នា `P(A|B) =frac{p ( A cap B )}(P (B)),(p(B) ne 0 )`
-
តាមរូបមន្តនេះគេអាចទាញបានប្រូបាបនៃព្រឹត្តិការណ៍ផលគុណ `A` និង `B`
`P(A cap B) = P(A) times P(B|A) = P(B) times P(A|B)`
`A` និង `B` ជាព្រឹត្តិការណ៍ 2 ដែលមានប្រូបាបមិនសូន្យ
-
គេថាព្រឹត្តិការណ៍ `A` និង ព្រឹត្តិការណ៍ `B` មិនអាស្រ័យគ្នាកាលណាព្រឹត្តិការណ៍ទាំង 2 ផ្ទៀងផ្ទាត់លក្ខខណ្ឌណា មួយក្នុងចំណោមលក្ខខណ្ឌខាងក្រោម :
1. `P (A cap B ) = P(A) times P(B)` ឬ
2. `P (A|B) = P(A) `ឬ
3. `P (B|A) = P(B)`
-
គេថាព្រឹត្តិការណ៍ A និងព្រឹត្តិការណ៍ B អាស្រ័យគ្នាកាលណា
`P(A cap B) ne P(A) times P(B)`
រូបមន្តប្របាសរុប : `P(B)=sum_{i=1}^n [ P( B|A_i) times P(A_i)]`
ទ្រឹស្តីបទបៃយេស : `P(A_k| B )=frac{P(B| A_k ) times P(A_k)}( sum_{i=1}^n[ P(B| A_i ) times P(A_i )])`